Differential Equations: some simple examples from Physclips

Differential equations involve the differential of a quantity: how rapidly that quantity changes with respect to change in another. For instance, an ordinary differential equation in x(t) might involve x, t, dx/dt, d2x/dt2 and perhaps other derivatives. We'll look at two simple examples of ordinary differential equations below, solve them in two different ways, and show that there is nothing frightening about them – well at least not about the easy ones that you'll meet in an introductory physics course. (And, by the time you meet difficult equations in second and higher year physics courses, you will have done more formal study of differential calculus in your mathematics subjects.) We assume that you already know a little calculus. If not, see this introduction first.

Methods for solving differential equations

    There are several different ways of solving differential equations, which I'll list in approximate order of popularity. I'll also classify them in a manner that differs from that found in text books.

    Know it or look it up. Of course! Very many differential equations have already been solved. Some of these you will learn, and others you can look up. This is by far the most common way by which scientists or mathematicians 'solve' differential equations. It is also how some (non-numerical) computer softwares solve differential equations.

    Substitution. Often a differential equation can be simplified by a substitution for one or other of the variables. This may turn it into one that is already solved (see above) or that can be solved by one of the other methods. (The software packages do this, too.) This category of solution includes a range of techniques that you will learn in a second year mathematics course.

    Guess and try. Another very common method of solving differential equations: guess what the solution might be, substitute it and, if it is not a solution, or not a complete solution, modify the guess until one has a complete solution. This is used often – more often than you would guess from reading books and papers, where the process usually appears to be rather elegant. In many cases you know something about the system studied, which gives you a clue. Experience helps, too, of course. However, we'll see below that the guessing is sometimes easy.

    Modify a simpler solution. If you know a solution to an equation that is a simplified version of the one with which you are faced, then try modifying the solution to the simpler equation to make it into a solution of the more complicated one.

    Transformation. Some differential equations become easier to solve when transformed mathematically. This is the main use of Laplace transformations.

    Numerical solution. If all the above fail, then an algorithm, usually implemented on a computer, can solve it explicitly, calculating the derivatives as ratios. This is usually a method of last resort, for two reasons. First, it only gives you the solution for one particular set of boundary conditions and parameters, whereas all the above give you general solutions. Second, it has limited precision: numerical derviatives are inherently noisy.

    Integration. This technique is elegant but is often difficult (or impossible). Sometimes one can multiply the equation by an integrating factor to make the integration possible.

    Special types. This vague title is to include special techniques that work for particular types of equations. This, too, is for study in higher year mathematics courses.

    Analog solution. Some differential equations are easily solved by analog computers. These are extremely fast and so suited to 'real time' control problems. Their disadvantages are limited precision and that analog computers are now rare.

    Below we show two examples of solution of common equations. They are simple, because they have only constant coefficients, but they are the ones you will encounter in first year physics. These equations could be solved by several of the means above, but we shall illustrate only two techniques.

Example 1: Exponential growth and decay
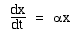
    One common example given is the growth a population of simple organisms that are not limited by food, water etc. Let the number of organisms at any time t be x(t). The rate at which new organisms are produced (dx/dt) is proportional to the number that are already there, with constant of proportionality α. So the differential equation is:
      equation

    Before going any further, what do we know already? Think what this situation means: If the number doubles in one day (say), then the second day there are twice as many available to reproduce, so the population will double again on the second day and so on. This tells us what solution we are looking for: geometrical or exponential increase (an example is sketched at right: more about the exponential function on this link).

    Because this is a simple equation, let's solve it by integration.

    For this equation, it is possible to separate the variables, i.e. to rearrange the equation so that one side involves only x and the other only t. Here, we obtain

      equation
      equation

    where C is a constant of integration. (More about the log function and constants of integration on Physclips calculus.) The constant(s) of integration are usually found from the boundary conditions: which in this case means from knowledge of x at some value of t. For this example, suppose we know that, at time t = 0, x = x0. Substitution gives

      equation

    The difference between two logs is the log of the ratio, so

      equation

    and, taking antilogs (or raising each side to the power of e):

      equation

    		plot of x=exp(t)
    plot of x=exp(t) Let's check the dimensions.

    eαt is a number, so x has the same dimensions and units as x0: that's good! The argument of the exponential function must be a number, so that means that a has the dimensions of reciprocal time. α is the proportional rate of increase in population, so it is a fraction per time, so yes, the dimensions are correct. Because of these dimensions, it is common to define  τ  =  1/α , which would give the solution

      equation

    In the example at right, τ (or 1/α) is called the time constant or characteristic time. Its meaning is now clear:  when   t  =  τ,   x/x0 is  e1  =  2.72. After two time constants have elapsed, (when  t  =  2τ), we have  x/x0  = e2 = 7.39 etc. x grows by a factor of e over each time interval τ. (More about the exponential function on this link .)

    Incidentally, it's worth stopping here to note that differential equations are almost always only approximations. It is impossible to have a system that is described this equation. For instance, the population of any species cannot grow exponentially. To quote just one limit: once the organisms occupy a solid sphere whose radius is increasing at the speed of light, any further growth cannot be exponential. (It is worth remembering this when politicians become obsessed with achieving growth in anything, but especially population.)

    plot of x=exp(t)

    Exponential decrease

    In the example above, α was positive. Consider now the case where the coefficient of t is negative, for which an example is radioactive decay. If there are N(t) radioactive nuclei at time t and N0 at t = 0, and if their rate of decay (-dN/dt) is proportional to the number of undecayed nuclei, with constant of proportionality α, then
      equation

    Doing the same integration as above, we have

      equation

    where in this case τ is the time taken for the population to change by a factor of  e−1  =  0.37, and so forth.

Example 2: Simple harmonic motion
    We look at Simple Harmonic Motion in Physclips, first kinematically (i.e. describing and quantifying the motion) then physically in Oscillations. In the latter we quote a solution and demonstrate that it does satisfy the differential equation. Let's look more closely, and use it as an example of solving a differential equation.

    In the x direction, Newton's second law tells us that F = ma = m.d2x/dt2, and here the force is − kx. This gives us the differential equation: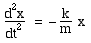

      equation

    where x is the displacement from equilibrium of the mass m at time t, and k is the stiffness of the spring to which the mass is attached.

    What do we know already? Now, even if we have never seen a mass attached to a spring, we can guess the behaviour. First the trivial one: if the mass is at rest and at equilibrium, then it will stay there.

    Behaviour. If we displace the mass and release it, the spring accelerates it towards the equilibrium position (x = 0). When it reaches there, the force on it is zero, but it is travelling with a non-zero velocity. So, because of its inertia, it overshoots: it keeps travelling, beyond x = 0. On this side of x = 0, however, the spring acts to slow it down, eventually bringing it to rest. But the spring force is now large, so it accelerates in the opposite direction, heading back towards x = 0. When it gets there, it overshoots... Okay, it oscillates. So we'll be looking for a solution that oscillates.

    Another point is that we neglected friction to arrive at this equation. So there is nothing to convert mechanical energy, so the system will oscillate for ever. That's important in our solution, too.

    Dimensions help as well. The left hand side is an acceleration so k/m must have dimensions of (time)−2. So the characteristic time τ in this equation is given by τ−2 = k/m or τ = (m/k)½. The reciprocal of time is frequency, so 1/τ might be the frequency, or perhaps the angular frequency, or at least related to them. We'll find out.

    This is a good time to use the Guess and try method of solution. We need a solution that oscillates forever, and that has the property that its second derivative is proportional to itself, but negative. The sine function does all that. Now we can't write x = sin t for dimensional reasons: the argument of the sine function can't have dimensions: it is given in radians (which is a ratio or number). We can write

      sin (2πft) or, equivalently          sin (ωt),
    where f is the cyclic frequency (the number of complete cycles of the sine wave per unit time) and ω = 2πf is the angular frequency (the number of radians per unit time).

    However, sin (ωt) is a number and we need a length to have the same dimensions as x, so a possible solution is:

      x  =  A sin (ωt)
    When we were describing simple harmonic motion, we called A the amplitude: the sine function varies from −1 to +1, so the motion varies from −A to +A.

    However, there is a problem with this proposed solution: it has x = 0 when t = 0. Which would be okay if I gave it a kick to start it from rest, but what if I release the mass from rest at a point away from equilibrium? In the latter case, I'd need x = A cos (ωt). The general solution must allow for these and any other starting condition. So instead we write:

      x  =  A sin (ωt + φ)

    Now, can it be a solution? We take the derivatives and get

      equation

    So it is a solution, provided that ω2  = k/m. Or, if you prefer, we can write the general solution as

      equation
    For elegance, however, we normally write
      equation

    So let's return to consider φ. If we start the motion (t = 0) with v = 0 at x = A, then φ must be 90°: we have a cos function instead of a sine. Alternatively, if we start with maximum (positive) velocity at x = 0, then we need φ = 0. We give examples of these cases on the background page for oscillations. However, we could start with any combination of initial displacement x = x0 and v = v0. So, for the general case (x0 ≠ 0, v0 ≠ 0), we can substitute to obtain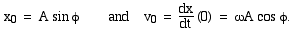

      equation

    We can solve these in terms of A and φ, first by dividing the two equations, then by squaring them and adding. So, for these given initial conditions, we can find a combination of the constants A and φ, so this is the general solution.

    How many boundary conditions? In our first example, we only had one constant of integration to find, so only one initial condition (or other boundary condition) to find. The second example was a second order equation, requiring two integrations or two boundary conditions. Here, we might specify two out of the initial displacement, velocity and acceleration, or some other two parameters.

Damped and forced oscillations
    Above we have solved the equation
      d2x/dt2 + ω2 x  =  0 ,      where ω2  =  k/m .
    Let's now add an extra term: the linear term in dx/dt. This gives the equation for damped oscillation:
      d2x/dt2 + β dx/dt +  ω2 x  =  0 ,      where ω2  =  k/m  and where β > 0.

    Physically, this term corresponds to a force, proportional to the speed. What can we guess about the solution, and how would we go about modifying the solution we had above so that it would satisfy our new differential equation? Again, we can use our knowledge of the physical system: when we a force whose direction is opposite that of the velocity, we slow it down. So we'd expect one of two possible answers: either it should oscillate, with the magnitude of the oscillations gradually decreasing over time, or else (if the damping were large enough) it could slow to a stop without even oscillating.

    This would suggest to us the possibility of a solution of the form x  =  A e−βt sin (ωt + φ). We can try this already. But it's not quite a solution. Well, what if the damping force slows down the vibration? Why not try (ω + δω) instead of ω = k/m and see if this gives a solution for a suitable value of δω?

    Let's add a further complication: let's start shaking the particle, with an extra oscillating force, say F = F0 sin Ωt. This gives us a new differential equation:

      d2x/dt2 + β dx/dt +  ω2 x  =  F0 sin Ωt.
    This is the equation for forced oscillation. What will happen if we let this system evolve until its behaviour is stable? Here again we can guess a solution,

    substitute into the differential equation and then try to modify it, or to choose appropriate values of its parameters. Why not have a try first and, if you want to check, go to Damped Oscillations and Forced Oscillations, where we discuss the physics, show examples and solve the equations.

Partial differential equations: the wave equation
    When we have a function y(t), we can readily define dy/dx as the slope of the plot y(x). But now consider y(x,t). In our example, this will be the displacement y of a point on a string as a function of position on the string x, and time t. So we can now think of two different derivatives. We write them differently. (We also introduced them in a section on the Calculus page.) What we shall do here is to solve the wave equation, the equation of motion for a wave in a string. (See Waves I and Waves II for an introduction.)

      ∂y/∂x. Think of this as dy/dx at a given, constant time, t. Imagine taking a photograph (time is constant): in the image at time t, this is the slope of the y(x) shape at the instant of the photograph.

      ∂y/∂t. Think of this as dy/dt at a given position, x. This is just the velocity in the y direction at a particular point x on the string. (Not the velocity of the wave, by the way).

    Let's take a standard example. A travelling sine wave with amplitude A, frequency f = 2πω and wavelength λ = 2π/k has the equation

      y  =  A sin(kx − ωt),    so
      ∂y/∂x  =  kA cos(kx − ωt),     which is the slope of the string at position x and time t, and
      ∂y/∂t  =  − ωA cos(kx − ωt),     which is the velocity of a point on the string at x and t.

    Now all of these three expressions are functions y(x,t): they are curves y(x) that change over time t. So the next animation plots them in this way (which is something that text books can't do!). You can pause the animation to check the slopes y(x) and you can also check that the velocity expression has the right shape.

    The bottom two graphs are the second derivatives with respect to the same variables:

      ∂y2/∂x2  =  − k2A sin(kx − ωt),     which is the rate of change in the slope of the string, as x varies, and
      ∂y2/∂t2  =  − ω2A sin(kx − ωt),     which is the acceleration of a point on the string.

    These have important physical significance: the first one is determines the curvature of the string. If ∂y2/∂x2 = 0, then the slope is constant, so it is straight. That means that the tension T acts in opposite directions at opposite ends, giving no nett force. If a segment is curved, however (∂y2/∂x2 ≠ 0), it has a force acting on it. For constant curvature over a small length L, the nett force is proportional to L.

    We know the acceleration so we can apply Newton's second law. The mass of the segment is μL, where μ is the mass per unit length μ. Writing Newton's law as a = F/m gives:

      ∂y2/∂t2  =  (T/μ)∂y2/∂x2  

    Looking back at our expressions for the two second derivatives, we see that they our original function y  =  A sin(kx − ωt) is a solution to the wave equation, provided that T/μ = ω2/k2. We also saw, in Waves I, that ω/k is the wave speed, v. Which finally relates the wave speed to the physical properties T and μ of the string:

      v  =  √(T/μ).
    The wave speed is greater if the string is stretched more tightly, and less if the string has a high mass per unit length.
Creative Commons License This work is licensed under a Creative Commons License.