| |
|
|
|
Newton's laws: background and limitationsNewton's laws are introduced in a multimedia tutorial: Chapter 5 of Physclips. This page gives some deeper and broader background. In particular, it addresses the philosophical basis and limitations to Newtons laws.
Newton's laws written in different ways
Newton's first law: Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.
Newton's second law: The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.
Newton's third law: To every action there is always opposed an equal and opposite reaction: or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.
Newton's first and second law combined: F = ma, where setting F = 0 gives the first law. As we've said, forces come in pairs that add to zero. For example, the force that I exert on my chair equals the force it exerts on me, or the gravitational force the earth exerts on the moon equals that exerted by the moon on the earth. Or, in general, for bodies 1 and 2, and for any interaction between them, Newton's third law: F1,2 = - F2,1 , or F1,2 + F2,1 = 0. For a body of finite size, one might ask what acceleration is meant. In this case, a is the acceleration of its centre of mass. We deal with this in one the centre of mass module on Physclips . We also deal with a more general version of Newton's laws in the modules on momentum and energy. Do Newton's laws apply? Inertial vs non-inertial frames
In the situation depicted here, if we neglect air resistance, both observers would agree that the ball, in flight, is subject to no horizontal forces. In the animation at left, Zoe, the observer on the merry-go-round, sees the ball accelerate in the horizontal direction, in violation of F = ma. In contrast, Jasper, the observer on the ground, sees no horizontal acceleration of the ball. He sees that the merry-go-round and the ball thrower are both accelerating due to their circular motion. So Jasper sees Newton's laws obeyed (to an excellent approximation), and explains Zoe's observation as due to the acceleration of Zoe's frame of reference. So, which is/are the frame/s of reference for which Newton's laws hold? Such frames are called inertial frames. Frames (such as Zoe's) in which Newton's laws do not hold are called non-inertial frames. Apart from conducting Newtonian experiments, is there a way whereby we may tell whether a frame is inertial or not? In fact there is: one looks at the distant stars. But this raises the subject of relativity, and the work of Galileo, Newton, Mach and Einstein. To pursue these ideas further, go to: Do Newton's laws work for different inertial frames?
This animation is also from our site on Relativity, where relative motion is discussed in greater detail. Briefly, however, let us derive the important result here, using the motion of the ball as an example. Suppose that the train is moving at velocity v, as measured by a person at rest in the station. Let's give this observer the x,y coordinates shown. With respect to that coordinate system (at rest with respect to the station), let the position of the ball be r. With respect to a point at rest with respect to the train (the origin of the x',y' coordinates), let the position of the ball be r'. Note that we use the dash to indicate measurements with respect to the train (eg x', y', r'). Let the origin fixed in the train have position p, as measured from the station in the x,y frame. 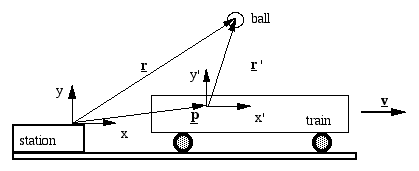 Now in the station frame, the velocity any point fixed in the train is v. Integrating with respect to time, its position r is given by
Now let's relate the measurements r and r' and their derivatives, remembering that r' is measured with respect to the x',y' frame.
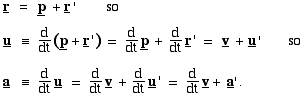 We assumed that, with respect to the station, the train is not accelerating, so the time derivative of v is zero. This gives us the important result
In other words, the two observers would obtain the same value for the acceleration of the ball. So, if the station is an inertial frame, then a = F/m, where m is the mass of the ball and F is the total force acting on it. If the two observers agree about the forces and agree about the mass, then they will have the same values of F and m, and we've shown that the both get the same value of acceleration: a = a'. So a frame of reference moving at uniform velocity with respect to an inertial frame is also an inertial frame. We have deliberately omitted mentioning one further assumption made above, and it has to do with taking time derivatives. We have tacitly assumed that the clocks in the two frames both measure the same time. If you did not notice this assumption, you are in good company -- it was largely unnoticed between the times of Newton and Einstein. However, this is one of the assumptions that must be considered when studying relativity. Which we do in the site on relativity. F = ma: Does it define F? define m? Is it a physical law? Can it possibly be all three?
What is F?The concept of force is a useful way of quantifying how an object interacts mechanically with its environment and vice versa and it is introduced for that reason. If two large masses are close to each other and far from others, we observe that they accelerate towards each other. Hence we define a gravitational force and quanitify it. Analogous observations are made concerning the other forces. As we saw above, by definition, a (nett) force is what makes a mass accelerate. So, how to quantify it? We can measure the size and direction of forces using F = ma. We can also compare two forces by 'balancing them', by setting F1 + F2 = 0: total force is zero so there is no acceleration (in an inertial frame). For instance, when we weigh an object on a balance, we are often adjusting a magnetic force until it is equal to and opposite the weight of the object. (In practice, there are often levers as well.) In a very convincing and pragmatic way, such measurements tell us all most of what we know about forces. What we know from observation is how an object interacts with its environment. It may accelerate or not. Sometimes we can feel forces: we can feel, almost directly, contact forces against our feet or against our bums on chairs. In most cases, however, we don't feel or observe forces directly. Forces appear in our models, ie in our explanations. They are usually somewhat removed from direct observation. Because forces are often a little removed from observation, their description could be said, philosophically, to be somewhat arbitrary.
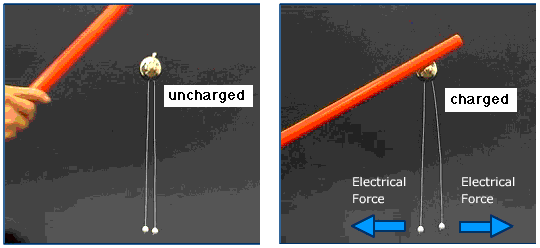 In this picture (from a background page in electricity and magnetism, we explain the observation in terms of an electrical interaction, but that explantion itself depends upon models for gravity and for the tension in strings. Sometimes forces are modelled as action at a distance and sometimes via fields (the two are logically almost equivalent). As we show in the module about energy, it is possible to make models that use distributions of potential energy and thus avoid the use of forces altogether. Again, in most cases, these different models are logically almost equivalent. (In the past, however, philosophers might have regarded these pictures as rather different: the Newtonian force picture looks like cause and effect, while the Hamiltonian energy picture looks more like purpose.) On the very small scale, forces are often analysed as the exchange of virtual particles. As a general rule, forces are less helpful as a model on the very small scale, in part because position, velocity and acceleration become poorly defined in that scale. See the uncertainty principle for more detail. What is m?
Gravitational mass, mg, on the other hand, could be defined by mg = W/g, where W is the object's weight and g is the local gravitational field. Galileo's famous experiments, David Scott's version shown below, and some much more sophisticated and precise experiments since then demonstrate that mg and mi are proportional, and therefore may be set equal by a choice of units.
However, there is no philosophical reason why Aristotle had to be wrong and Galileo right: as everywhere in science, only experiment and observation tell us that. Philosophically, mg and mi could be different*. That the proportionality is not a coincidence is Mach's Principle. That the two are indistinguishable -- the principle of equivalence -- is a starting point for Einstein's theory of General Theory of Relativity, which is Einstein's theory of gravitation. * The Pioneer 10 and 11 space probes are now further from the sun than Neptune. The Pioneer anomaly is a tiny difference between the apparent acceleration of these deep space probes during the later stages of their trajectories and the acceleration calculated from the gravitational effects of planets, tidal effects, pressure of light against them and some other small effects. Some researchers think that this difference is due to calculation errors, others think that new physical principles are involved. Some have proposed that non-Newtonian mechanics may be required to explain the difference. Yes, but what is m really?
Many physicists suspect that an as yet undiscovered field, the Higgs field, plays a role in determining the mass of some fundamental particles. It is the particles' interaction with the Higgs field that would determine, in some cases, their masses. Associated with the Higgs field is a particle, the Higgs boson, which can only be created by energies that are just beyond the reach of nuclear experiments performed to date. The Large Hadron Collider at the Centre Européen pour la Recherche Nucléaire (CERN) was built in part to create* Higgs bosons and to measure some of their properties. We may know more about mass when and if "the Higgs" is discovered. However, even with out the Higgs, we can say something about the origin of mass. If this theory turns out to be correct, then it will explain the mass of the electron but only a small fraction of the mass of the neutron and proton (which are a couple of thousand times more massive than the electron). In fact, most of the mass of neutrons and protons (and thus most of the mass of ordinary objects) is probably due to an effect that, while still exotic, is much better understood than the Higgs field. Many physicists suspect that most an ordinary mass m is just E/c2. Saying this is just a rearrangement of Einstein's famous equation E = mc2. Mass and energy are either interconvertible (via the very large conversion factor c2) or, for some theorists, the same thing. Quantum chromodynamics (QCD) analyses how the 'ordinary' nuclear particles such as neutrons and protons are made from quarks, which interact via the chromoelectric field carried by gluons. (There is a limited analogy here with quantum electrodynamics, which analyses how protons and electrons interact via the electric field carried by photons.) According to QCD, nearly all of the mass of neutrons, protons and most nuclear particles is due to the energy of the different distributions of quarks and antiquarks which, because of quantum uncertainty, cannot ever cancel out each other's colour charge completely. (See E = mc2, Energy in Newtonian mechanics and in relativity and the uncertainty principle for further background). Exactly how this works is not known. The energies depend on how quarks and gluons are confined, and QCD itself does not give a scale for confinement -- currently, this is introduced empirically. Perhaps this scale comes from the Higgs field interaction too. Some suspect that it may have something to do with dark matter. This may be resolved fairly soon. Nevertheless, it seems very likely that most of your mass is in fact the energy stored in neutrons and protons in the different configurations of their quarks and gluons. Of course that doesn't tell us what energy is. Physclips has a module on energy, but there we relate it to forces, so, while I think that the module does tell a lot about energy, you might justifiably accuse me of circular reasoning if I claimed that this settled the matter. Further, QCD doesn't tell us the mass of the electron and it doesn't account for quite all of the mass of neutrons and protons either. Some readers may be helping here: if you pay taxes in Europe, then you are helping fund the Large Hadron Collider and thus the search for the Higgs boson. Nevertheless, we can put particle physics aside and say that mass (and, at least to some extent, its other self, energy) are defined by Newton's second law, in one of its forms. Hence my perseverence in showing that F = ma really can define mass and force, as well as being a testable law. And if you find this unsatisfying, it's worth noting that there will always remain departure points in physics, just as there are postulates or axioms as the departure points in mathematics, just as there are postulates or axioms as the departure points in mathematics. * So, how do you create a Higgs boson? The LHC will accelerate two beams of either protons or lead nuclei in opposite directions in storage rings 27 km long. At speeds of about 99.99999% of c, they will collide. Much of their kinetic energy will be converted into particle-antiparticle pairs. Including sometimes, it is hoped, the elusive (and massive) Higgs. It's a big project. For instance, the LHC needs 100 tonnes of liquid helium just to keep the magnets cool. What if m varies?
What, then, if mass varies? In this case, we use the more generalised version of Newton's first and second laws, using the definition of momentum p = mv. We then write Newton's first and second laws thus:
which of course reverts to the familiar F = ma for constant mass. We discuss this in the module on momentum. In very many cases, the second term is negligible. Keep in mind, however, the possibility that you may need the equation above in some cases. Newton's third law
Forces always come in pairs, and the sum of the pair is zero. You'll often see this law written as 'To every action there is an equal and opposite reaction'. The trouble with that statement is that it leads to some confusion: 'action' and 'reaction' suggest that one of the forces comes first and the other comes later. In most situations, however, the forces are completely symmetric. I push against the wall, means that there is an electrostatic repulsion between electrons in my hand and electrons in the wall. There is nothing special about my electrons that makes their force an action and the wall's force a reaction: there is the completely symmetrical electrical repulsion between electrons. All three laws in one equation
(And, as a speical case, if no external forces act on a system, then its total momentum is conserved.) This more general law is, so far as we know, completely true. There is even an odd sort of argument that suggests why it should be true: see Newton's third law and the anthropic principle. However, just as F = ma does not apply if m is not constant, we should point out that Newton's third law does not apply if some effects are omitted. For instance, if we consider the magnetic interaction between two moving charges, in the general case the forces do not add to zero. In such cases, relativistic effects and the momentum of radiation caused by accelerating charges must be included.
Conclusion
These caveats made, however, we note that, on the macroscopic scale and over the vast range of practical energies and forces, Newton's laws work spectacularly well and are the foundation of a large fraction of physics and engineering. And, if you are going to work on the scale of very small or very high energies, then you'll simply have to learn some quantum mechanics and some relativity -- which will be fun, too! At the end of the chapter on mechanics, there is a section in which we are quantitative about the limits to Newtonian mechanics. Demonstrating Newton's laws with a spring and a bowling ballThe film clips below use a spring to accelerate a bowling ball. You can tell whether the spring applies a force from whether it is stretched or not, as in these photos. Use the step frame button on the film clips.
Example: Circe and circular motion
See also Newton's laws: more background
|
|
|
||||||||
F = ma really does define force and define mass. Either one of these seems at first glance to make it a tautology - something that is true by definition. And yet it is, as the name implies, a scientific law and therefore, in principle, falsifiable.
Remember the problem in the multimedia tutorial? The man says to the horse "Giddup" (which is horse for "go"). The horse replies: "There's no point. Newton's third law says that the cart will exert a force on me equal and opposite to the force I exert on it. Sum of forces = zero, so the acceleration will be zero."
How would you answer the horse?
