Graphs, errors, significant figures, dimensions and units
This page supports the Physclips project,
especially Chapter
2: Projectiles
The first chapter in Physclips mechanics uses displacement-time and velocity-time graphs for a man walking in a straight line, so we'll begin with this animation.
An example: Displacement-time graphs
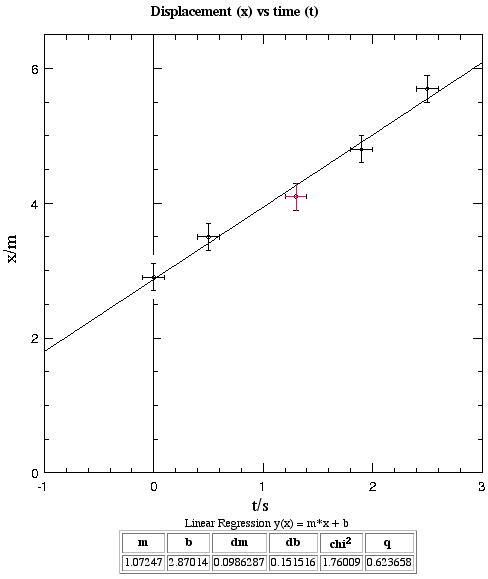
How can we keep track of this fellow? In other words, how do we show his position at any time? The graph above answers this question. The man's distance from some reference position, here the wall, is how far he is displaced from it. We call this displacement x, where x is positive if he is to the right of the wall. Formally, the graph shows his position as a function of time.
The reference for displacement is the wall, x = 0. We also need a reference for time. It could be the time at which we set a stop-watch ticking. If the watch starts at zero seconds, any time after that is positive time (t > 0). Of course physics was still happening before we set our watch, so anything that happens before t = 0 would be represented on the negative part of the time axis.
Units on graphs
In science and engineering, the fundamental units for length and time are metres (abbreviation m) and seconds (s). Multiples and submultiples (kilometre, microsecond) are used when needed. There are two common ways of representing units on the axes of graphs (here m and s). One is to write x (m) and t (s). The disadvantage with this convention is that it may suggest that x is a function of m, and it is awkard when one really does want to plot x as a function of m. The method used here is to plot x/m and t/s. This has the advantage that, when x is divided by a metre or t is divided by a second, the result is a number. Numbers (not quantities) are what we plot on the axes: the axes really are x/m and t/s, so it is a good idea to to label them in this way.
Errors, error bars and significant figures
How accurately are the data known? Suppose you make the measurement x = 4.1 m by looking at a tape measure. As you do so, you click the stopwatch, which shows 1.32 seconds. It is difficult to define the position of a person with greater precision than about 0.2 m, because of the relative motion of arms and legs, so the error in the measurement is likely to be roughly this, or greater. We should therefore write x = 4.1 ± 0.2 m.
We might be tempted to write t = 1.32 s, because the watch is capable of measurements with this precision. You will probably find, however, that you are not. Repeated measurements of the same period (eg the time it takes a second hand to pass 2 seconds on a clock) will not usually give the same answer, and the variation is probably about 0.1 s. So the measurement error here is (very roughly) about 0.1 s. Now, if you write t = 1.32 s, you are implying that the '2' means something, that it is significant. You are implying a precision that you don't actually have. So, to avoid misleading the reader, you should retain only the two significant figures. Consequently, this should be written (as we say) to two significant figures, t = 1.3 s. To make the error explicit, we might write t = 1.3 ± 0.1 s. (If we had done a detailed study of our timing reproducibility and found its standard error to be 0.15 s, we could write t = 1.32 ± 0.15 s.)
How can we show the point (t,x) = (1.3 ± 0.1 s, 4.1 ± 0.2 m) on a graph? We do this by drawing a cross, whose vertical axis goes from 3.9 to 4.3 m and whose horizontal axis goes from 1.2 to 1.4 s. This is shown in red on the graph at right.
Slopes of graphs
In the example shown, the data are well fitted by a straight line (given as m±dm in the table) whose slope can be determined with reasonable accuracy.
Here, that means constant velocity. But what if the velocity varies with time? Can we take the slope of the graph between each two points? The problem with doing so is that a given absolute error in measurements becomes a large proportional error when the difference is small. For example, consider the first two points on this graph. The time difference is 0.5 ± 0.2 s, a maximum error of 40%. There's also a large error in the difference in x, leading to a very large error in the calculated velocity.
What to do? If we think that the acceleration might be fairly constant, then we could try fitting a parabola to the data. If we don't know what sort of model might fit the data, then the best we can do is take larger intervals in time. If we take the slope from the first to the third measured point, we get a more reliable estimate of the velocity, but we now have less precision in the time at which that velocity occurred. This is a fundamental limitation. There are a number of ways to try to get around it, but they all have limitations. One way is to try several curves fitted to the data and then to choose the best. With this best curve, we take the derivative and plot that for the velocity.
|
Units and dimensions
What is wrong with saying
- "My height is 45°C"? Or:
- "The game lasted 15 kg"? Or:
- "The displacement is given by the weight divided by the volume squared"?
In each case, we mention two physical quantities that cannot possibly be equal. Let's take the first: a height cannot equal a temperature, so I cannot measure my height in degrees Celsius. Let's call my height h. I can say "h = 1.8 m". I can also say "h = V/A", where V is my volume and A is my average horizontal cross sectional area. In both cases, the quantity on the right hand side is a distance, as is the quantity on the left hand side. Both can be measured in metres.
We shall see that this very simple idea can be quite important – and also very useful.
Now the units on either side of an equation need not be the same. For instance, I may write
This equation is true. (In fact, it is the definition of the inch, a unit of length in the old British system of units.) However, this equation is different from the silly examples given above, because both the millimetre and the inch measure length. We say that both sides of the equation have the dimensions of length. This condition must be satisfied for an equation to be true, or even to make sense. Further, if equations have different units with the same dimension, appropriate conversion factors must be included, as is the case above.
Let's look at more interesting examples. When we write
we are specifying that the dimensions of force are those of mass times acceleration. The dimensions of acceleration are length, which we write as [L], divided by time [T] squared, so we write, just for the dimensions:
In the units of the Système International, almost universally used in science, there are no conversion factors for the base units, so we can relate the newton, the unit of force, to other base units:
And to use our equation once more, we note that, while mass is a scalar, force and acceleration are both vectors, so our previous equation tells us not only that F = ma, but that F is parallel to a.
Let's now see how the method of dimensions can be useful, via this Example: how does the frequency, of a pendulum depend on the length?
We know that this depends on the length, L – a long one swings more slowly than does a short one. It also depends on the strength g of the gravitational field – it won't swing at all without one. Does it also depend on the mass, m? On the temperature, T? Let's write for the frequency, f:
where N, a, b, c and d are numbers, yet to be determined. Of course, we can analyse the dynamics of the pendulum and determine them, but let's see how far we get just by considering the dimensions. Frequency has units of "per second" so it has the dimensions of reciprocal time, T−1 . So, setting the dimensions equal on both sides, we have:
T−1 = N.La.(L.T−2)b.Mc.Temperatured
For this equation to be true, each dimension must occur, to the same power, on each side. So, considering each dimension, the exponent gives us an equation to be satisfied. If we start with time T, we see that it appears to the −1 power on the left, and to the −2b power on the right, so we have
where the arrow means "implies". For the other dimensions, we get
Now the last two shouldn't surprise us. A more massive pendulum experiences a greater gravitational force but it also requires more force to accelerate, so we should not be surprised that the dimensions of the problem tell us that c = 0, ie that these effects cancel out: the frequency does not depend* on the mass of the pendulum. Similarly, we see that d = 0, but we should not be too surprised that a hot pendulum and a cold one swing at the same frequency -- unless of course the temperature changes the length perceptibly.
The other two equations tell us that b = 1/2, and that a + b = 0, so a = −b = −1/2. So, substituting in our original equation for the frequency,
f = N.L−1/2.g1/2 = N(g/L)1/2.
We still don't know the value of the number N, and cannot get it from the information we have been given here. (It is 1/(2*π), in case you were wondering.) However, we do know that, all else equal, the frequency is proportional to the reciprocal of the square root of the length. To halve the frequency of pendulum, make it four times as long.
* I raise a couple of tiny caveats, to preempt the pedants. For a pendulum whose mass is comparable with the that of the planet upon which it is mounted, the pendulum mass does appear -- or at least the ratio of these two masses appears. Further, we have cheated a little on the temperature, because we could write temperature in units of energy. Doing so, the conversion factor would be Boltzmann's constant, whose very small size would give us the clue that temperature is only relevant in mechanics for objects of molecular size. And on this molecular scale we should often need to use quantum mechnics rather than Newtonian mechanics.
Other units
With rare exceptions, scientists use the SI system of units. (SI stands for Système International d'Unités.) This system is based on the kilogram for mass, the metre for length, the second for time, the ampere for electric current, the kelvin for temperature, the mole for chemical quantities and the candela for luminous intensity. Other systems are the British imperial system and natural units.
Physclips is a scientific presentation, and we use only the SI. If you enounter problems stated in other units, the simplest procedure is often to translate the problem into SI, solve it, then translate the back. This sounds like extra work, but it is usually much less than the extra work required in using the imperial system of units, which has internal conversion factors.
In the United States of America, Liberia and Myanmar, the British imperial system is the official system. This system used to be much more widespread, and vestiges of it remain in other countries that are in the process of 'going metric', ie converting to the SI.
Dealing with or converting from the imperial system usually involves just a multiplictaive factor. For instance, the inch, an imperial unit of length, is officially defined to be equal to 25.4 mm. These multiplications can become awkward in some cases: consider this imperial unit of thermal conductivity, one British Thermal Unit per second per square foot per degree Farenheit per inch. One can see why it exists, but it is ugly and inconvenient. (For comparison, the SI unit thermal conductivity is W.m−1.K−1.)
Some confusion arises, however, because of the different colloquial use of units of mass and force in the SI and imperial system. In the imperial system, the unit of force is the pound-force, or sometimes, as in many American physics text books, just the pound. The unit of mass in the imperial system is the slug, which is a mass that is accelerated by one pound at one foot per second per second. The slug is 14.5939 kg. These equations, which are definitions, allow us to compare the units of mass and force:
SI
Unit of force = 1 newton = 1 kg.m.s−2
Imperial
Unit of force = 1 pound = 1 slug.foot.second−2
In imperial units, the gravitational acceleration is 32 feet.second−2. Consequently, a slug weighs 32 pounds.
The slug is very rarely used. Pound is used colloquially as a unit of quantity – a pound of apples colloquially means a quantity of apples that weighs a pound-force (at the earth's surface). There is another imperial unit of force, the poundal. This is defined as the force required to accelerate at one foot.second−2 a mass whose weight is one pound. So a pound is 32 poundals.
The units mentioned above are related to features of the earth (its circumference originally determined the metre, and the second is related to the day) or of artifacts on earth, such as the standard kilogram, or of particular substances, especially water. In contrast, the laws of physics and combinations of them yield natural units, which are used by some theoretical physicists, especially cosmologists. The speed of light, for instance, is taken as the unit for speed. Although this makes equations look simple these units are, in general, inconvenient for measurement. For instance, the natural units of length and time are inconveniently small (The Planck length is 1.6 x 10-35 metres, the Planck time is 5.4 x 10-44 seconds). See The Planck scale for more detail.
|

