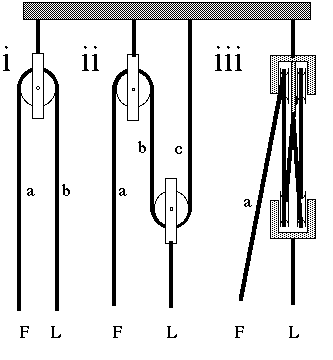
| Diagram (i) shows a pulley being used just to change
the direction of a force. You can pull on the end of rope marked a
with force F and the end b moves an equal distance with load force L
(neglecting friction).
(ii) shows an arrangement that doubles the force. You pull with
force F on the section a. Again neglecting friction, the sections of
the same rope marked b and c are also under tension F, so the second
block is pulled up by 2F, so the load lifted L = 2F. This extra
force does not come 'free', however. When you pull a distance x on
a, x is the total amount of shortening in both b and c, so each of b
and c is shortened by x/2, which is how much the load L rises. The
work you do is Fx, the work done on the load is L.x/2 = Fx.
In (iii), pulling on a causes four sections of the rope to
shorten and to share the load. So these blocks multiply the force by
four times, but you have to pull 4 times as far.
|
|

