Centre of mass
The centre of mass depends on the distribution of masses in a body or system. Here we derive Newton's laws in terms of the centre of mass and illustrate them with film clips. This page supports the multimedia tutorial Centre of Mass |
|
|
We've seen in projectiles the path of an object in free fall in a uniform gravitational field: it's a parabola. That's fine for a single particle, but what about for an extended object? Look at the path traced by a point on the end of a rod shown in the film clip below left. It's definitely not a parabola. In fact, this rod is rotating as it travels, so there is a centripetal acceleration as well as the vertical acceleration −g.
The clip at right, however, shows that there is a point whose trajectory is a parabola. That point is the centre of mass. (In a uniform gravitational field, the centre of mass is the same as the centre of gravity, which is illustrated by the inset photo.)
Things look even more complicated if the extended object is not rigid. Is there a parabolic trajectory in the clip below?
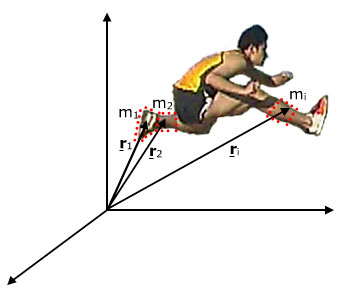 Let's start with the definition of the centre of mass. For this, let's consider the extended object as a collection of particles. (In one sense, the object is a collection of neutrons, protons and electrons. However, for our purposes here, we can usually consider dividing it into much larger elements.)
(This section is not yet finished. Apologies.)
|
On the figure below, the centre of mass is identified. Once his feet leave the ground, the only external forces acting on him are gravity and air resistance.
An obvious question is how we identified the centre of mass in making the images above. The answer is quite low tech: we used a flexible plastic model of a man, we bent it into the approximate shape of the hurdler in each frame, then we balanced it on a bar in two directions, taking the intersection as the centre of gravity and thus the centre of mass.
|
