Mexican wave: how fast and how stiff is it?
A Mexican wave or stadium wave is a good example of a vertically polarised, transverse, travelling wave. The wave travels in the horizontal direction, the 'particles' whose motion comprises the wave move in a largely vertical direction. The wave direction and the particle motion define the plane of polarisation.
Here we report some measurements done to have a value of speed and stiffness, and investigate a variation polarised in the horizontal plane, and longitudinal waves. A periodic boundary condition was used. This experiment was by no means serious, and cannot be considered a laboratory trial: it was a participation event in Orientation Week at UNSW in 2010. This page exists to initiate discussion, which can be continued on the Physics Questions bulletin board.
Wave speed vs particle speed
It's interesting to compare the speed of the wave itself with the speed of the particles whose collective motion makes up the wave. Anyone who has seen a wave travel around the Sydney Cricket Ground in less than a minute will have deduced that the wave can travel rather faster than the average speed of the 'particles' whose collective motion produces the wave.
In this example, the wave made two complete circles in 14 s, while the runner (seen here trailing the pulse) took 20 s. At this stage, the circle of people has a circumference of 40 m and comprises 32 people, giving a wave speed of 5.8 m.s−1. The runner travels an extra 6 m or so, so his speed is 4.6 m.s−1.
(Photos courtesy John Smith)
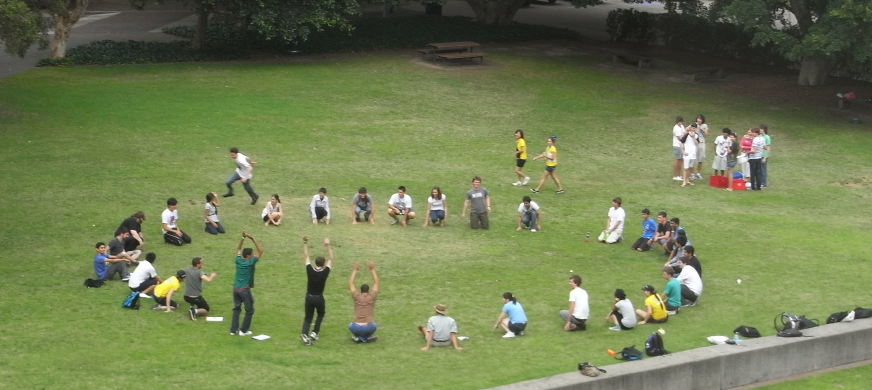
|
| |
Stiffness
In Travelling waves II, we saw that the speed v of a wave in a stretched string is:
where T is the tension in the string and the mass per unit length is μ. This specific example demonstrates some general features. Usually, it is possible to write an expression for the speed of a wave like this
There is a restoring property that tends to return displacements to their equilibrium value. For the string, this is the tension T. To get a wave, there must also be something like inertia. Consider the moment when a vibrating guitar string is instantaneously straight. Here, its inertia carries it past equilibrium. For the wave in a stretched string, the
inertial term that appears the mass per unit length is μ.
(For sound, the relevant inertial property is the (three dimensional) density ρ, while the restoring property is the atmospheric pressure times a the adiabatic constant γ, which is about 1.4 for air. So the speed of sound is (γ*Patmosphere/ρ)½.
To extend this to electromagnetic waves, we could say that the electric field has a restoring effect, because electric fields produce forces that tend to move the charges that created the field in a way that reduces the field. The magnetic field has something like an inertial property, because changes in the magnetic field produce electric effects that tend to maintain the magnetic field. So we would write that the speed of an electromagnetic wave should be the square root of the ratio of Coulomb's constant for electricity to Coulomb's constant for magnetism. Here is a discussion of the speed of light in this context.)
Like the string, the wave here is quasi-one-dimensional. Take an average mass of 70 kg per student and we have a line density of μ = 60 kg.m−1. Rearranging our equation to give
restoring property = (inertial property)*(wave speed)2
we obtain a 'restoring property' whose value is 2.4 kilonewtons. This is larger than the weight of a typical participant. How do you think it compares with the force required to stand up in order to be part of the wave? What other relevant parameters do you think might be involved in the speed of the wave? For instance, the participants here are seated on the ground, while those in a typical stadium are often on seats. Might this make a difference?
From this photo we could also estimate that the pulse width in this model wave is about 3 m.
Tunnelling: the Members Stand Effect
Stadium waves sometimes exhibit a process analogous to evanescent coupling or quantum tunnelling.
For example, the Sydney Cricket Ground has a section called the Members Stand, to which are admitted only a group of persons whose inertia appears to be higher than average. They do not rise to participate in the wave, possibly because of the weight in their wallets. Nevertheless, the wave seems to 'jump' across the impenetrable barrier, a little like an evanescent wave in optics or quantum tunnelling in, say, nuclear decay or a tunnel diode.
To investigate this, five people, placed consecutively in our sample, sat and pretended to be Members (no further instructions were given). This gave a prohibited region of length 4 m. The time that the wave took to 'jump' this barrier was 2.6 s, giving a notional wave speed of about 1.5 m.s−1.
|
Polarisation

|
Here we observe a wave pulse with horizontal polarisation. At this stage, the circle had grown to 42 m and contained 41 people, so its line density was about μ = 70 kg.m−1. However, a rather fraction of the mass took part in the displacement than was the case for vertical polarisation. Two complete circles now take 14 s, so the wave speed is approximately unchanged, despite the (small) increase in line density with respect to the vertically polarised wave.
restoring property = (inertial property)*(wave speed)2
we obtain a 'restoring property' whose value is 2.4 kN. Again, it is interesting to compare this with forces involved in displacing and restoring the torsos from and to the equilibrium position.
|
Longitudinal

|
For the remaining cases, the circle had accreted two more people to become 44, but retained the length of 42 m, giving an estimated μ of 70 kg.m−1.A wave in a string is, like the two waves previously discussed, a transverse wave. Sound, however, is a
longitudinal wave: the displacment of air is parallel to the propagation of the sound wave. These two photos show longitudinal wave pulses: compression above and tension below. The average speeds recorded were 4.8 and 3.4 m.s−1 respectively.
|

|
One more experiment (not pictured) had the entire circle hold hands. One of the people then squeezed the hand of his neighbour, who squeezed the hand of her neighbour, etc. This wave travelled at 5.2 m.s−1.
Finally, we should repeat that the exercise was more for fun than for serious measurement. Some of the new particles joining the medium did not have the same sample preparation (i.e. explanations) as the original sample. This probably had significant effect on the results.
Further discussion may be continued on the Physics Questions bulletin board.
|
|

