Waves, power and radiation |
Power in a wave
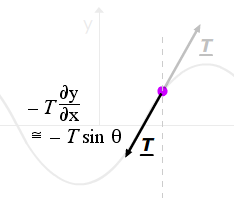What is the rate at which the string to the left of a given point is doing work on the string to the right? Let's assume that our travelling wave is, as usual, y = A sin (kx − ωt) . From the definition of work W, a force F does work F.ds, and dividing by dt gives the power P, or rate of doing work:
Because the amplitude is small, we are considering only y motion. The component of the force in the y direction is − T sin θ and the vertical and the velocity in the y direction is ∂y/∂dt so, using the small angle approximation for θ,
We have already seen the partial derivatives above, and substitution gives:
Using v2 = T/μ to substitute for T, we have an expression for the power at any instant t:
Over a whole number of cycles, the average of the cos2 function is ½, so the average power transferred from the left to the right, for a wave travelling to the right, is
Note the dependence on all of the terms:
The rate of transmission of energy to the right is
- proportional to the speed v at which the wave shape is travelling to the right,
- proportional to the mass per unit length μ
- proportional to the square of the angular frequency ω
- proportional to the square of the amplitude A.
The appearance of the squared terms is logical. Remember that, for the travelling sine wave, each point on the wave executes simple harmonic motion with amplitude A and angular frequency ω. So the kinetic energy ½ mv2 is proportional to μA2ω2. |
Intensity
|
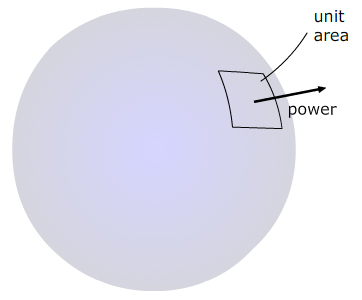For a wave in one dimension, as seen above, power is transmitted at a point, from the continuum to the left to the continuum to the right. For waves in three dimensions, power is transmitted through an area, which is why we introduce the intensity I, defined as the power per unit area.
For a simple case, imagine a small source of power P, which is radiating waves isotropically, which means equally in all directions. For examples, we might think of a small source of sound high up in the air, or a small lamp as a source of light. At a distance r, all of the radiated power is radiated through a sphere with area 4πr2. So the intensity at r from the source is
However, this equation should be used with caution. Few radiators are isotropic. Further, measurements are usually complicated by reflections. |
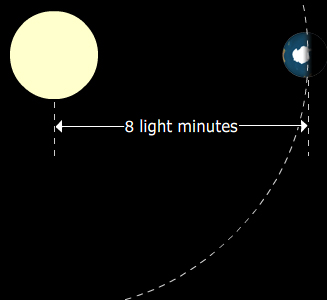This is a simple example, using a radiator that is very close to isotropic: the sun. Above the earth's atmosphere, the intensity provided by the sun is 1.4 kW.m−2. This quantity is well known to those working with solar cells, although the intensity recorded at ground level is inevitably lower. The earth is 8 light minutes from the sun (another memorable quantity). So we can work out the power output P of the sun:
= (1.4 kW.m−2).4π(8 minutes*speed of light)2 = 4 x 1026 W
|
We saw above in Power in a wave that the power transmitted is proportional to the square of the amplitude. The intensity of a sound wave is proportional to the square of the amplitude (pressure or velocity) and the intensity of an electromagetic wave is proportional to the square of the amplitude (electric field or magnetic field). So any of these amplitudes (pressure or velocity for sound, electric field or magnetic field for an electromagetic wave) are proportional to 1/r in the spherical radiation case such as the one we've just discussed.
Radiation in three dimensions
If one stays a reasonable distance from reflecting surfaces, measurements of intensity are easier to interpret. For sources of sound, if the wavelength is much larger than typical dimensions of the source, then the source is often a reasonably isotropic radiator. (Try some examples in the experimental section.) Here is a simple demonstration. The sound track, recorded from a microphone held in my hand, is displayed below. Remember that the intensity goes as the square of the amplitude (for sound, this is true of both pressure and displacement amplitudes).
|
|
For light, it is easier to avoid reflections: black surfaces reflect little light. A light bulb is not isotropic, but is reasonably uniform over a wide range of angles.
|
|
Radiation in two dimensions
If you watch a ripple spread on the surface of water, you will see the amplitude decrease. Here, the total energy associated with the disturbance is spread out over a circular circumference, so the energy in a pulse goes as 1/r. All else equal, one would expect the amplitude to go as 1/√r, but because the shape of the wavepacket changes, the situation is more complicated.
This link has more movies of waves on water surfaces – and more jacaranda flowers.
|
|
Reflection in two dimensions
|
Reflections become more complicated in two and three dimensions, where they occur at a line and a surface respectively. Usually, the phase of the incident wave varies with position on the reflecting boundary, and the reflected waves interfere with each other and the incident wave.
This animation shows simplified reflections in two dimensions. They are a little like what one would get from an oscillating stick in water near a rigid wall. This is an analogue of Lloyd's mirror and Young's experiment. However, it is only an animation: the small angle approximation, among others, has been made.
We shall discuss interference effects in a later chapter. |
|
Multimedia tutorial: Waves I
Multimedia tutorial: Waves II
This link has more movies of waves on water surfaces – and more jacaranda flowers.
|
