Analysing the brick problem

The 2 kg hammer has a considerable kinetic energy: if it travelled at 10 m.s⁻¹, its energy would be ½mv² = ½(2kg)(10 m.s⁻¹)² = 100 J. If the hammer collided directly with my chest, this energy would be transferred directly to several square centimetres of my chest: it would break ribs and cause other damage. How is damage avoided in this example? Let's analyse it quantitatively, but first discuss some key points qualitatively:

• First, only a small fraction of the kinetic energy of the hammer is transferred to the plank.
• Second, the force is not applied locally, but via hundreds of nails over the whole of my chest.
• Third, my chest is not rigid, but somewhat flexible. This means that that plank, brick and hammer travel downwards, compressing my chest. This finite movement means that the force required to stop them is not extremely large.
• The bed of nails adds to the circus flavour, but it's the simple part of the problem. As we'll see below, the upper bed of nails increases the comfort and safety of this process.

One of the great strengths of physics is that it is quantitative. For this problem it is not enough to know that a force would compress my chest. Here, I really did want to know how big the force would be and how far it would compress my chest!

Safety and precision. As you can imagine, this is a case where I did some calculations before doing the experiment, so let's look at them more closely. However, let's note that this is a calculation in which confidence is important, but precision is not. I don't care whether the force is 400 N or 500 N – either would be comfortable. I do care whether it is 400 N or 4000 N – the latter would be dangerous. (400 N is the weight of a child, 4000 N is the weight of several adults.)

This problem is worth analysing carefully for you, too. First, it's a problem in which someone's life, or at least comfort, depends on the outcome. Scientists and engineers are sometimes called upon to do such calculations. Second, it's a problem with several steps, and it's useful to get practice in analysing such problems. Third, it uses some important principles. Divide the problem into parts. First there is a collision. During a collision, we can usually neglect external forces and apply conservation of momentum. After the collision, the hammer, brick plank of nails and part of my chest are all travelling downwards. How far will my chest be compressed? What is the maximum force applied? In the chapter Weight and Contact Forces, we observed the compression of my chest under a steady, known load. We also saw that, when the load was removed, my chest returned to its original shape – no hysteresis. This suggests that it is approximately elastic and that the force involved is almost conservative. So we can approximate the chest's behaviour as that of a spring, with negligible nonconservative forces. (For a few cm, it is approximately a linear spring.) So, for the second part of the problem, we can apply conservation of mechanical energy – approximately, at least – to get an estimate of the magnitude of the forces and displacement involved. Now a rugby player might be confident that someone can stand on his chest without breaking bones, but I preferred to do a calculation first. Working out the force to break the bones would be difficult but, if I hold my breath, then the air in my lungs acts like a spring. So, suppose my lungs contains air, initially at atmospheric pressure PA= 100 kPa. Suppose that the load of say 1 kN is distribued over an area of ~0.1 m2, giving an extra pressure ΔP = ~10  kPa. So the pressure increases by 10%. Now, would the compression be approximately adiabatic or isothermal? Although it is rapid, the alveoli are very small and gases mix and diffuse in them in seconds, so isothermal would probably be a good approximation, rather than adiabatic. So, at constant temperature, PV = constant. So I'd expect the lungs to be compressed by in volume by only 10%, even if the strength of the ribs didn't help. Of course, the shape may change as well but, if the compression is all in the vertical direction, my chest would compress in height by less than 10%, so I'd only expect a compression of a couple of centimetres. This won't break my ribs. So this gives me a very rough estimate of the spring constant of the air in my chest, and thus an underestimate of that of the chest including the air. In Weight and Contact Forces, we measured it as well. (Incidentally, I find it rather interesting that the spring constant of my chest should depend, over long time scales at least, on whether my glottis—the aperture in my larynx—is closed or open!)

 

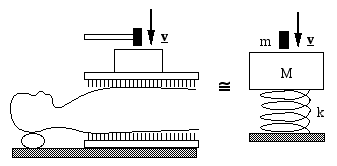
Drawing diagrams. It is very often helpful to draw a diagram, especially a simple one that retains the important physics. The first sketch here is pictorial. It is still too complicated. The schematic diagram at far right includes several useful simplifications and assumptions. The handle of the hammer has little mass, so I treat the hammer as a single rigid object, mass m, travelling downwards at speed v before the collision. The brick and the upper bed of nails move together, so I have combined them as a single mass M. The lower bed of nails is mainly to make it more dramatic, so I omit it (the force on my back will include a fraction of my weight, but the impulsive force will be small because of the inertia of my torso). Then I replace my chest by a spring, for reasons mentioned above.

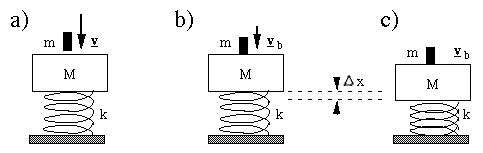Now comes a very important part of the analysis: 'before' and 'after' diagrams. Even the simplified diagram above is not enough. For conservation problems, we usually need a 'before' and 'after' diagram. Here, both stages of the problem (collision then chest deformation) require 'before' and 'after' diagrams, so I draw three diagrams representing (a) the objects just before collision (b) the hammer, brick and plank immediately after collision but before compressing the chest and (c) the chest at maximum compression, with hammer, brick and plank stationary. (a) and (b) are the 'before' and 'after' diagrams for the collision, (b) and (c) are the 'before' and 'after' diagrams for the phase involving compression of the chest.

Collision: steps (a) to (b)
External forces do act during the collision: the weight of the brick, for instance, is 180 N. To neglect this weight requires a little thought. First, we know that the brick can, without breaking, support forces much greater than its own weight: the bricks at the bottom of a wall are supporting the weight of many bricks (and other loads) above them. The force required to break the brick is much greater than 180 N. So, in comparison with the forces that act during the collision (which breaks the brick), the weight of the brick and plank, for example, are small, so we shall neglect them.

Before we write equations, let’s define some variables: Let the mass of the hammer be m, and v its velocity (downwards) just before the collision. Let M be the mass of the brick, plank, hammer plus the section of my chest that moves with them. The velocity of M is zero before the collision. After the collision, suppose* that M is traveling downwards with velocity v_b.

Conservation of vertical momentum from (a) to (b) is then written:

Total initial momentum  =  total final momentum

mv + 0  ≅  Mv_b.    So

v_b ≅  mv/M        (1)

In this case, the mass of the hammer is m = 2 kg. The mass of the brick is 18 kg, that of the plank is 12 kg and I guess that several kilos of tissue moves with them.  So  m/(m + M)  =  1/17. This is important: I shall be hit by an object travelling more than ten times slower than the hammer.

* Note that there is an approximation when I say 'suppose* that M is traveling downwards'. If the hammer bounces upwards from the brick, then it will have upwards momentum after the collision, so the downwards momentum of the brick and plank would be greater. The hammer cannot bounce back with more than its original speed, so this error cannot be greater than a factor of two. Further, if the hammer hits hard enough to break the brick, it will not bounce back much, so the error is only important for soft hammer blows, which are of less interest. That's why I say 'ten times' rather than 'seventeen times'.

A further consideration is the force required to accelerate the tissues of my chest to approximately the speed of the plank. Collisions involving soft objects are usually relatively slow, but let's say that 10 kg of tissue accelerates to a metre per second over a few hundredths of second. That requires an average force of a few hundred N. Spread over a few hundred nails, this won't pierce the skin.

Loss of energy in this inelastic collision

If all of the momentum of the hammer is transferred to the combined mass, then conservation of momentum tells us that the velocity is reduced by a factor m/M. The kinetic energy is mass times velocity squared. So the kinetic energy of the combined mass is less than that of the hammer alone by a factor of m/M. So the collision loses more than 90% of the energy – this is good news for me!

Deformation of the chest: steps (b) to (c)

After the collision, the plank+brick+hammer are travelling downwards. How far will this depress my chest? As discussed above, my chest behaves approximately as a spring. The proportional deformation is small so, if we assume it's a linear spring, we can give it a spring constant. My assistant's weight is between 500 and 600 N. When she stands on the plank on my chest (see Weight and Contact Forces), it is deformed by roughly 20 mm, so my chest acts approximately like a spring with a constant k ~ (600 N)/(20 mm) = 30 kN/m. (Incidentally, I can vary k substantially by holding or not holding my breath and by tensing or not the muscles in my chest, so this is yet another rather approximate value. Interesting that it is of the same order as the value of k estimated above.) So now we examine the compression phase that follows the hammer-brick collision: from diagram (b) to (c). Because the chest compression is approximately reversible, it's probably roughly elastic, so mechanical energy is approximately conserved. So (Uspring + Ugrav + K)initial  = (Uspring + Ugrav + K)final. Let the chest compression be Δx, and remember that there is gravitataional potential energy as well as that of the spring. So this equation becomes: ½kx12 + 0 + ½Mvb2 + = ½k(x1+Δx)2 − MgΔx + 0 , which we rearrange to get ½Mvb2 = ½kx12 + ½kΔx2 + (kx1 − Mg)Δx − ½kx12, We use the mechanical equilibrium before the collision kx1 = Mg      and simplify to have Δx2 = Mvb2/k        (2). Then use equation (1) to substitute vb = vm/M and relate x to the impact speed v of the hammer and the other parameters: x2 = Mvb2/k  =  M(mv/M)2/k          x  =  mv/(kM)½       (3). Let’s check a few things, because this is an important calculation! First, the units. (If necessary, revise Units and dimensions) k is a force per unit length (kg.m.s−2 per m = kg.s−2) so the units are kg.m.s−1/(kg.s−2.kg)½ = m, so yes, the right hand side is a length. Let’s check the way it depends on the different terms: a large m (big hammer) will compress the chest further. Good. A large M (heavy plank or brick) reduces the amount by which the hammer compresses the chest. A stiff spring is compressed less. All these are as expected. Note that the bed of nails actually makes this stunt easier in one sense: because it contributes to M, it reduces the expected compression of the chest after the collision, and thus (provided it's not enormously heavy) the maximum force I'll feel.

How fast can someone swing a hammer?

10 m.s⁻¹ is rather fast – the speed of a sprinter or of a hammer dropped from 5 metres. It's hard to move your hand much faster than that without practice. To accelerate a 2 kg hammer to that speed over half a metre requires a force of 200 N. So I used 10 m.s⁻¹. In fact, the video shows that Sue swings it at about 4 m.s⁻¹, but better safe than sorry. (Another safety note: the plane of her hammer swing is such that, if the hammer came out of her hands or the head came off, it would pass over my right shoulder. No people were in that plane, except me, and I had a bed of nails to protect me.)

So substituting this large speed in (3) gives Δx ~ 20 mm.

With the value of k (30 kN.m⁻¹), this gives a maximum force shortly after the collision of 600 newtons. This is about Sue's weight, and I've already tried that in an earlier chapter, when we measured k.

Some safety considerations

So there is a big safety margin here. (I assure you, I shouldn't have done the demonstration without one!) This is good, because there are some rather rough approximations above. So, even if the hammer travelled at 10 m.s−1 (factor of three), the force would still be only 600 Newtons. Also, I need to consider what happens if the hammer misses the brick, in which case a smaller fraction of its energy is lost in the collision, the plank rotates and the force is concentrated more locally. Sue and I both need to worry about flying bits of brick (hence the goggles for Sue and face mask for me). And I asked her to hit the end further from my face: even with the full face mask I'd rather have lumps of brick land on my legs than my head. It's important, too, to disinfect the nails – especially if someone else has been using the bed of nails. Finally, even if you have understood all of the calculations and considerations above, don't try this at home! This problem is a good teaching exercise, so I've done it in class. Here is a lecture theatre version of the brick smashing problem, live in class (posted by a student on Youtube).

Nails

These add a bit of circus flavour to the demonstration, but they also have an educational purpose: the indicate the importance of being quantitative. The nails are sharp. But a steady force of a few tens of newtons on a single sharp nail is not painful. My weight is 700 newtons. If I distributed the weight over several hundred nails, the force on each one is quite small. Caution is required, however, to avoid concentrations of weight and sudden accelerations. More importantly, as noted above, the upper bed of nails protects me from a stray hammer and its mass appears in the demoninator when calculating the force applied just after the collision.

The ballistic pendulum

If you view the video clip in the multimedia tutorial, you will note that the pendulum rotates about its support, and also flexes. Both of these motions store some kinetic energy, as we'll discuss in Rotation. For this analysis, however, we'll neglect it.

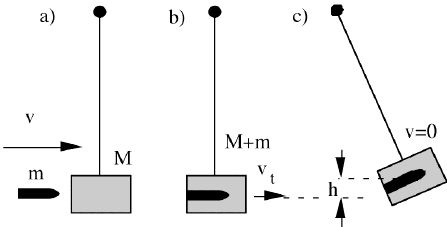This schematic divides the process into two stages, with before and after diagrams for each: (a)-(b) is a completely inelastic collision between a small mass m with initial speed v and a larger mass M. After the collision, the speed of the combination (M+m) is vt. During this collision, which has short duration, external forces are negligibile in comparison with the internal forces. Consequently, momentum is conserved. This is followed by the rise of a pendulum ((b)-(c) in the schematic), a process during which external forces are not negligible and during which momentum obviously is not conserved – the pendulum comes to a stop at the top of its motion. However, during (b)-(c), nonconservative forces do negligible work. So in this phase we can use the approximation of conservation of mechanical energy. (a) - (b): a completely inelastic collision Here, conservation of momentum in the x direction gives us: pxi = pxf      so mv = (M + m)vt . (b) - (c): pendulum rise – conservation of mechanical energy Uinitial + Kinitial  = Ufinal + Kfinal. Making the approximations mentioned above, and taking the lowest point as the zero for potential energy, this equation becomes: 0 + ½(m + M)vt2 = (M + m)gh + 0 . Combining the two equations allows us to relate h to v: h = ½m2v2/(M+m)2g . We should check the dimensions of the expression. Then the dependence on the parameters: higher v gives larger h. Larger ratio (M+m)/m gives smaller h. Larger g gives smaller h. All as expected. We can now rearrange this equation and use the measured value of h to estimate the initial speed v. v = ((M+m)/m)(2gh)½. I am told that, before the age of high speed cameras, this was a useful way of measuring the muzzle speed of a rifle. I am also told that one of my predecessors, a professor at UNSW, used to do such a measurement as a lecture room demonstration. Don't try that at home, either: imagine the consequences if the collision were not completely inelastic.

Similarities between these problems

Of course there are differences: the objects involved are different, the ways of storing potential energy are different and that second difference gives a different algebra. However there are underlying similarities: An inelastic collision. A phase with conservation of mechanical energy. Similar approximations made. Have another look at the multimedia tutorial and look for these similarities.

You may want to return to the multimedia chapter Momentum on Physclips.