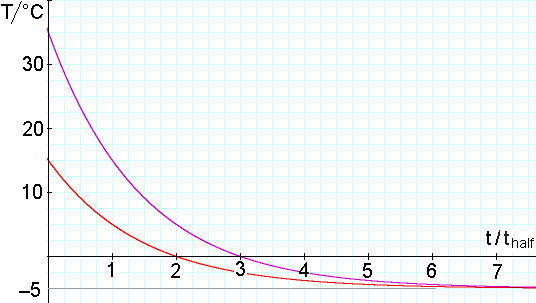snowgums in the snow: photo

The Mpemba effect: why hot water can sometimes freeze faster than cold

It is possible that, under certain circumstances, a sample of hot water can take less time to freeze than a sample of cold water. Superficially, this may seem surprising. Here we explain how this is possible.

Potential artifacts

Supercooling

    More importantly, hot water is unlikely to have the same composition as cold water. Water is almost never pure H2O. It usually contains dissolved gases, minerals and trace compounds, some of biological origin. These impurities change the temperature at which freezing occurs. In some cases, very small quantities of certain impurities (called ice nucleators) could increase the temperature at which freezing occurs by several degrees or more.

    Very small changes in composition can have a big effect because of the phenomenon of supercooling. This effect requires a bit of explanation. but first, let's define:

Equilibrium freezing

Ice nucleation and freezing point elevation

    The spontaneous freezing temperature depends strongly on the presence of ice nucleators: objects (including ice crystals themselves) upon which molecules of water can, one by one, form the structure of an ice crystal. Some bacteria produce molecules which are good ice nucleators. It is difficult to remove all ice nucleators from samples of water and the containers in which one intends to freeze them.

    Different samples of water can contain different types of ice nucleators. Further, these may be affected by heating the water. So two different water samples can have different spontaneous freezing temperatures. Further, the formation of the first ice nucleus is a probabilistic event, so the same sample can have different spontaneous freezing temperatures in successive experiments.

Typical experiments

    Now let’s consider a typical freezing experiments. Especially in informal situations, such as a high school science project, such experiments are often conducted in freezers at temperatures not far below 0 °C. We’ll now see why this is very important.

Newtonian cooling

    The rate at which heat is lost depends on temperature difference. Under many conditions, the rate of heat loss is approximately proportional to the temperature difference between sample and surroundings (called Newtonian cooling). If the temperature of the surroundings is constant and if there is no freezing, melting, boiling or other changes of phase, Newtonian cooling approximation leads to sample temperature approaching the surrounding temperature exponentially over time. (More about this approximation below.)

    For an example, consider a freezer at say − 5.0°C and suppose that a small sample cools from say 35 to 15°C: in other words the temperature difference ΔT between sample and surroundings decreases by half (ΔT goes from 40 to 20°C). We call this the cooling half time thalf. Because of the exponential cooling, it takes the same time, thalf, to cool from − 1°C to − 3°C (ΔT goes from 4 to 2°C) or from − 4.8 to − 4.9°C (ΔT goes from 0.2 to 0.1°C).

Numerical examples

    Supercooling and slow approach to final temperature together explain why very small differences between the composition of two samples of water (or quite small artifacts) can have a relatively large effect on the time they take to freeze.

    graphs showing Newtonian cooling from 35 and 15°C with same half-times The next example shows why. Again, suppose that our freezer is at − 5.0°C. Further, let’s suppose that one sample (A) freezes at − 4.5°C (ΔT = 0.5°C) and another (sample B) freezes at − 4.9°C (ΔT = 0.1°C). The second sample’s freezing temperature is four times closer to the freezer temperature so, if the two samples started from the same initial temperature, the second will remain unfrozen for longer, by a time of 2*thalf.

    Now, remember that it takes only one thalf for the samples to cool from 35 to 15°C. So sample B could start at 35°C and sample A from 15°C but sample B would freeze first. This is the situation depicted in the graph.

    Why would the freezing temperatures be different? It could be chance: perhaps one sample has more effective ice nucleators than the other – and remember that it only takes one nucleator to initiate freezing. Further, because some of the nucleators are biochemicals, it is possible that even moderate of heating one of the solutions might change the effectiveness of the nucleators.

Non-Newtonian cooling

    For a number of reasons, Newtonian cooling is often only a rough approximation to cooling a container of liquid in a freezer. One reason is that larger temperature differences promote more vigorous convection. At higher temperatures, this brings warm water to the surface, allowing more rapid heat loss than would be possible without the vigorous convection.

    At low temperatures, however, the behaviour is different. The maximum density of water occurs at 4°C, so water at colder temperatures tends to rise to the surface, which is why lakes and rivers freeze from the top, rather than from the bottom. A layer of ice across the top of the container acts as an insulator and slows further heat loss.

    Convection accelerates the early part of the cooling of warm or hot samples. The formation of a cold layer at the surface could slow the later part. These effects therefore may contribute to the Mpemba effect.

More possible artifacts

    We should remember the potential importance of artifacts, of which we’ve mentioned one above. There are others: in a typical freezer, the air temperature and the radiation temperature both vary from one place to another, so similar samples at different points may have different rates of heat loss, particularly as they approach their final temperature. Different containers may them selves have different nucleation temperatures. Different preparations of samples may produce different nucleation properties. Nucleation is also probabilistic and history dependent, so repeated freezing of the same sample may produce different freezing times.

    Now look at the graphs above, and see how close the two curves are after several times thalf. This proximity means that even small artifacts may also play a role in determining which sample freezes first.

Freezing point depression

Further interesting effects

pic of superheated water

Joe Wolfe / J.Wolfe@unsw.edu.au /61-2-9385 4954 (UT+10,+11 Oct-Mar)
School of Physics, The University of New South Wales

Creative Commons License This work is licensed under a Creative Commons License.