
Freezing point depression and boiling point elevation: the effects of
solutes and of pressure
Freezing point depression is the lowering of the equilibrium freezing
or melting temperature by solutes in the liquid phase. Solutes in the
liquid phase also raise the equilibrium boiling temperature. Pressure also
affects freezing temperature (a little) and boiling temperatures (a lot).
This page gives a simple, non-mathematical explanation of all these
effects. Although the phenomena are more general, water is given as the
familiar example, because of questions such as:
- What happens to boiling and freezing when you add solutes (eg sugar
or salt) to water?
- Why do they salt the roads when it snows?
- How does antifreeze work?
- How can living tissues survive subzero temperatures?
- Can you make good tea on a mountain top?
- Do skates work by depressing the melting temperature of ice?
(For those looking for formal treatments, these effects
are analysed in standard second year physics courses under the headings
phase equilibria and the Clausius-Clapeyron equation, which we quote here
without derivation.)
Why do substances melt and boil?
To oversimplify only a little,
temperature is a measure of how much energy there is in molecular motion.
To begin with an explicit example, let's consider water. When water
molecules are cold enough, they don't have much heat energy so they don't
jostle around too much. Consequently, they can pack together in a very
organised structure, called ice. At high enough temperatures, they have so
much energy that they can escape the attraction of their neighbours. So
they form steam, in which the molecules fly all over the place in a very
disordered way. At medium temperatures, which means that the molecules
have moderate amounts of energy (and if the pressure is high
enough*) they form liquid water. Here the molecules have enough energy
to move around, but not enough to escape from their neighbours entirely.
Molecules in liquid water are more ordered than in steam but less ordered
than ice. (As an example of the order in a liquid, we can observe that the
centre of each molecule is about one molecular diameter away from that of
its nearest neighbours.)
Why is the change so sudden? At atmospheric pressure, water melts at
0°C and boils at 100°C. What determines the melting point and the boiling
point?
The answer is a trade-off between the molecular energy (which we notice
as temperature) and the molecular order: the difference between highly
organised structure in ice, rather close packing in liquid water, and
nearly complete disorganisation in steam. At 0°C and 100°C, the order
effect and the energy effect are exactly balanced, and so ice and water
co-exist at 0°C, water and steam coexist at 100°C (at atmospheric
pressure).
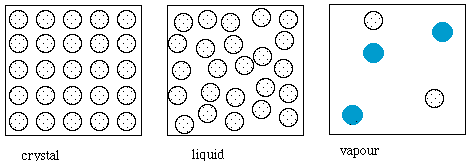
The crystalline structure of ice is rather difficult to show in two
dimensions, so the sketches below show, schematically, a simpler
crystal, liquid and vapour phase. The patterened circles represent
simplistically the substance in whose melting and evaporation we are
interested. The coloured circles represent molecules of the air, which
is mainly nitrogen. The black circles (next picture) represent solutes.
The sketches are not to scale.
The effects of solutes
What happens if, instead of having pure
liquid water, we put some salt or sugar in the water? In other words, what
if our liquid phase is a solution? This makes the liquid state less
organised, because the sugar molecules or salt ions are free to move about
almost randomly. So the liquid water molecules are more disordered (less
regimented) in a solution. The ice and the steam remain unaffected,
however: sugar and salt hardly dissolve at all in ice, nor do they
evaporate near 100°C.
How does this affect the trade-off between the molecular energy and the
molecular order? The gain in disorder on evaporation is now less, because
the liquid water in solution is more disordered. The energy effect is
hardly changed, so the energy effect now dominates over a slightly larger
range: the molecules of water in solution have to have slightly more
energy (a slightly higher temperature) in order for the two effects to be
in balance. So the boiling temperature is higher for a solution.
Conversely, when we look at melting, the disorder effect is greater for
a solution: on melting into a solution, water molecules go from the high
order of crystalline ice into an even more disordered state than pure
liquid. So the disorder effect can dominate even at lower temperatures. So
the freezing temperature is lower for a solution.
I mentioned the equilibrium freezing and boiling temperatures above. Time to explain. Imagine ice floating in pure water at 0°C. If we add a little heat, some ice melts. Remove a little heat and some water freezes. We call this the equilibrium freezing temperature: 0°C for water. However, when one cools reasonably pure water, it usually cools several degrees below 0°C – we say it supercools by several degrees – before the first ice crystal appears. That ice crystal then expands rapidly, giving up latent heat, which warms the nearby water back to about 0°C. More about supercooling and super heating below.
An aqueous solution has a higher boiling point and a lower freezing
point than does pure water.
If the solution is not too concentrated,
these two effects are approximately independent of what the dissolved
substance is: a sugar molecule has much the same effect as a salt ion. So,
provided you remember to count each ion separately, the effect of
concentration on boiling point elevation or freezing point depression is
much the same for all small solutes in water. (Macromolecules such as
polymers behave differently because they have lots of neighbouring solvent
molecules, and so affect the solvent much more than simple solutes.)
Antifreeze. So, you might expect that the antifreeze in a
radiator not only stops it freezing, but also helps stop it from boiling.
However, the real situation is more complicated: antifreeze has the
disadvantage that it is not quite as good as water at transporting heat.
Ethylene glycol is one antifreeze. Salt is used to melt snow and ice on
roads in cold countries, but it is not used in radiators because it is
corrosive and crystallises readily. Sugar is not used in some
applications, because concentrated sugar solutions are viscous, and
because they support bugs. However, many organisms use sugars and other
small organic molecules as antifreeze. See cryobiology.
An interesting observation: The concentration of solutes in blood is less than that in sea water, so the equilibrium freezing temperature of blood is usually higher than that of sea water. Consequently, some Arctic and Antarctic fish live at temperatures below the equilibrium freezing temperature of normal blood. The bio-antifreeze in their blood is a protein that works in a way different from the anti-freeze used in car radiators: the antifreeze protein binds to freezing nuclei and so permits the blood to remain supercooled.
The effect of pressure
Notice that above I've included the proviso
"at atmospheric pressure" a few times. The reason why the pressure is
important is that, in the vapour phase, a given amount of a substance
occupies a much larger volume than it does as a liquid. Some of the energy
required to vapourise it goes towards 'pushing the air out of the way' to
make room for the amount evaporated. (The amount of work done is the
product of the pressure P and the change in volume ΔV. Technically, there
is a PΔV term in the latent heat.) So, at low pressure, it is easier to
form the vapour phase and so the boiling point is lower. The dependence of
the transition temperature on pressure is the Clausius-Clapeyron effect.
(Again, being a bit technical, we note that this effect involves energy -
the work done in displacing air - whereas the solute effect involves
entropy - the disordering of the liquid phase.)
Water expands a lot when it boils: one kilogram of water is one litre
of liquid water, but it becomes about 1700 litres of steam at atmospheric
pressure. This means that even modest increases in altitude can measurably
reduce the boiling temperature. Some people complain that this affects
cooking and even the taste of tea at altitude.
It is also true that pressure changes the melting temperature. However,
because the volume occupied by a kilogram of liquid is not much different
from that occupied by a kilogram of solid, this effect is very small
unless the pressures are very large. For most substances, the freezing
point rises, though only very slightly, with increased pressure.
Water is one of the very rare substances that expands upon freezing
(which is why ice floats). Consequently, its melting temperature falls very slightly if pressure is increased.
I have been asked: Does freezing point depression
with pressure explain the low friction under an ice-skate? I'm writing this in Sydney, so you might guess correctly that I don't know much about skating, but let's try to be quantitative. The Clausius-Clapeyron equation says that the
ratio of the change in pressure times the change in specific volume to
the latent heat of the phase change equals the ratio of the change in
transition temperature to the (absolute) melting or boiling temperature.
It's often written as dP/dT = L/T*Δv. (As we might have
guessed from dimensional considerations — i.e. just writing an equation involving the relevant parameters so as to make the units correct.)
The weight of the skater is say 1 kN. I'm not a skater, but let's start with an estimate of the skate-ice contact area as say 100 mm2. (The value depends on how far the skate cuts into the ice. Say 200 mm long by 0.5 mm wide: skaters, is this reasonable?) So, with this value, the pressure is increased by (1 kN)/100 mm2 = 10 MPa or 100 atmospheres. A kg of water (one litre) freezes to give
about 1.1 litre of ice, so the change in specific volume is about
10-4 m3kg-1. The latent heat of
fusion of ice is 330 kJ.kg-1. So the proportional change
in temperature is
(10 MPa)(10-4 m3kg-1)/(330 kJ.kg-1),
which is 0.3%. Multiply this by the melting temperature of ice (273 K)
and, for this area, we get an estimate of the temperature change of around 1 K = 1 °C. So, with
these values, the calculation suggests that the pressure of an ice skate
would reduce the melting temperature of ice by about
1 °C. So, with this estimate for area and if this were the cause of the slipperiness, ice
skating would be possible only at temperatures only one or a few degrees
below freezing. From observation, it is possible to ice skate on ice at
much lower temperatures than this. To argue that freezing point depression works over say 10°C, we'd need an area
of contact of a skate about 10 mm2 or less. If only the sharp edges were in contact with the ice, this might be possible, but it seems very low to me, because the pressure on the ice would be 100 MPa or a 1000 atmospheres, and with this stress I'd expect the edges to cut into the ice and to increase the area of contact. (Again, I seek advice from skaters on this, and preferably from physicists who are also skaters.)
Putting aside the Clausius-Clapeyron effect, and under conditions with only small applied pressure, we'd expect the surface of ice is already somewhat
slippery. At the surface of ice, water molecules are only have opportunities for hydrogen
bonds to their neighbours 'on one side', as it were. Consequently, their energy is
not as low as in bulk ice. So, at equilibrium, they must have a higher
entropy. So, even at subzero temperatures, ice must have a thin water-like layer on the surface, whose
thickness woud be expected to increase at temperatures close to melting. [PS. Some years after writing this, I'm happy to report that a recent scientific study supports the idea of the surface layer of ice making it slippery, rather than freezing point depression.]
The comparable calculation for boiling point change is a bit more
complicated. The latent heat in this case is larger
(2.3 MJ-1) but the change in specific volume is much
larger (typically a few times
10-2 m3kg-1). So changes in
altitude can change the boiling temperature, and going up a mountain can
reduce it by as much as several degrees.
When are the boiling temperature and freezing temperature
equal? What happens then?
For all substances, as we lower pressure, the boiling
temperature falls much more rapidly than does the freezing temperature.
(For water, the freezing temperature rises slightly at low pressure.)
Hence the obvious question: Are the boiling temperature and freezing
temperature ever equal?
The answer is yes. At the low pressure of 611 Pa (only 0.006 times
atmospheric pressure), pure water boils at 0.01 °C, and it also
freezes at 0.01 °C. The combination of conditions (P, T) =
(611 Pa, 0.01 °C) is called the triple point of
water because, at this pressure and temperature ice, liquid water and
steam can coexist in equilibrium. This point is used to define our scale
of temperature: by definition, the triple point of water occurs at
273.16 K, where K is the kelvin. 273.16 K = 0.01 °C
* This explains why, above, I wrote that liquid water only exists if
the pressure is high enough. At pressures below 611 Pa, there are
only two phases, and ice sublimes to form steam directly, without passing
through a liquid phase. (In this context, the reverse of 'to sublime' is
not, as one might have hoped, 'to ridicule'. At low pressures, steam
condenses to form ice.)
|

