
 |
|
|
Car Physics: some problemsCars provide examples for several areas in physics. This page uses the car pictured for a few simple examples to illustrate the chapters Constant acceleration, Weight and contact forces and Energy and power. It also has example problems posed to us about cars. We'll add more later.

UNSW's solar racer sunswift IV on its way to winning the silicon division of the transcontinental World Solar Challenge.
Acceleration, speed, time, distanceFirst, a warning. The first two examples below assume constant acceleration – which is usually a chapter in introductory physics books. First, the forwards acceleration of a car is rarely constant. Motors rarely deliver force or torque that is independent of speed and drag is a strong function of speed (v) – turbulent drag is approximately proportional to v2. Deceleration can often be rather closer to constant, especially in hard braking and at speeds low enough that the drag may be neglected in comparison with the braking force (strictly, the horizontal force exerted on the tires by the road) or the rolling resistance (which is not stronly dependent on speed). Often, however, a rough estimate is sufficient answer, and that's what the first examples below provide. For precise answers, however, still more detail is required, as we indicate. Second, a note about units. Discussing cars, speeds are usually given in kilometres per hour, for obvious convenience in everyday life. However, accelerations are usually given in m.s−2 and, in any case, scientists and engineers usually work in SI units. A kilometer is 1000 m and an hour is 3600 s, so one k.p.h. is 1000 m/3600 s, which is (1/3.6) m.s−1. So, to convert k.p.h. to m.s−1, divide by 3.6. To convert km per hour to (land) miles per hour, divide by 1.61. Approximate drag example (using the constant acceleration approximation)
Force and powerForce. From Newton's second law, we write F = ma. Including a driver (and ballast, to make the effective driver's mass 80 kg), sunswift's total mass is 244 kg. Substitution gives a force of − 23 N. As we mentioned above, the drag force is not independent of speed, so neither is the acceleration. Nevertheless, we can say that this is greater than the force at 50 k.p.h. and less than that at 70 k.p.h. For now, let's guess that this is roughly the stopping force at 60 k.p.h. If she were travelling at a constant speed of roughly 60 k.p.h. in a straight line, the acceleration would be zero and so would the total horizontal force. So the drive wheel would have to apply a force of magnitude 23 N to the ground. (Only the single back wheel drives, and the motor is in the wheel to minimise losses in the drive train.) This doesn't sound like much: it is about the weight of a 2.3 kg mass, which you can comfortably apply with one finger – to an object at rest. Applying this force at a speed of 60 k.p.h. is less easy. Let's see why. Power. In the chapter Energy and Power, we saw that the power P applied by a force F applied at angle θ the direction of motion of a point moving at speed v is
Here θ is zero for a horizontal force, so substitution gives P = 380 W. A very fit human can supply 380 W for sustained periods, and rather more for short periods. (sunswift IV can supply rather more than this, too, especially if it's a clear day and the sun is high in the sky. More on this below.)

UNSW's solar racer sunswift IV on the Hidden Valley racetrack in Darwin, before the World Solar Challenge. Stopping example
Substituting, we obtain a = − 10.5 m.s−1. So her braking acceleration is a little greater than g. With mass 244 kg, this gives a total stopping force of magnitude 2.6 kN Brakes and friction. Compared with 2.6 kN, the 0.023 kN we calculated above for the coasting trial (at higher speed) may be neglected. So the stopping force is almost entirely that applied by the road to the wheels, which in this case includes regenerative conversion: the wheel motor becomes a generator and turns some of the car's kinetic energy back to electrical energy, which is stored in her battery. (There is also a rolling resistance, but this also is small (rather less than 1% of the braking force). As we saw in Weight and Contact Forces, this requires a limiting coefficient of static friction greater than unity. Values as high as 1.2 or 1.3 can be achieved on a clean road in dry conditions, but don't count on being able to stop this rapidly in general, even if the road looks clean! Air resistanceIn many cases, the turbulent drag is proportional to v2, to a good approximation. Roughly speaking, the car accelerates a mass of air near it, doing work in the process. In its turbulent wake, the kinetic energy of that air is dissipated as heat. Suppose the car travels dx in time dt. Suppose that, in doing so, the applies a force F to the air, and the magnitude of F equals that of the air resistance Fdrag (the force the air applies to the car – Newton's third law). This force F accelerates a volume of air to the speed v of the car, which has cross section A. We'll now look in turn at the questions: What is the mass dm of that air? How much work is done moving it? What power is required? What is the drag force? 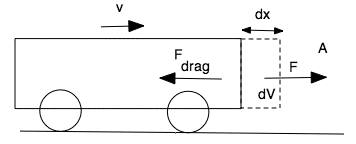
How much air is moved? First, imagine a non-aerodynamic vehicle, like a city bus. One might expect that, as the bus moves forward dx, it accelerates a volume dV, as in the sketch. Let's start with a crude approximation: let's say the volume accelerated is dV = Adx. If the density of the air is ρ, then the mass of air is ρAdx. How much work is done moving it? In our crude approximation, all of that air is accelerated to v, so its kinetic energy is ½mv2 = ½(ρAdx)v2. In practice, not all of that air is accelerated to the speed of the bus: some slips around it. Further, for carefully designed shapes, only a modest fraction might be accelerated – the rest is pushed aside. So let's combine those two effects (fraction of air in front of the vehicle accelerated and the fraction of v to which it is accelerated) in a single constant, CD, called the drag coefficient. It is a pure number, which we expect to be about one for a bus and rather smaller for an aerodynamic shape like that of the solar racing car. So the work done accelerating the air is ½CD(ρAdx)v2 What power is required? To get the power required to do this work in time dt, we divide by dt. Putting dx/dt = v, we get:
Drag coefficient and rolling resistanceWhat is the drag force? Let's again use the equation P = Fv cos θ, where again θ is zero for horizontal forces and velocity. So, dividing both sides of the previous equation by v, we have
Which looks fine... except that we don't know CD: we said above it was 'a number that is about one for a bus and rather smaller for an aerodynamic shape'. In other words, it's what we call a fudge factor. This particular fudge factor is called the drag coefficient. It is defined by the equation just derived, i.e. CD = Fdrag/(½ρAv2). However, although it looks like a tautology, it's still a useful equation, because CD is fairly constant – it depends only weakly on v. So, once we know CD from data on one or more speeds, we can predict the drag force for other speeds. The rolling resistance is approximately independent of v. So we have
So we need to quantify a few parameters. The second term above dominates at high v, the first term at low v. So at low v, the deceleration without motor and the car's mass tell us the rolling resistance, which is approximately independent of v. We can just plot v against time and the slope at low v gives us the rolling resistance. To get the drag force, we consider high v, and write
where k = ½CDρA/m. Let's now multiply both sides by dt/v, which gives us
We know that d(ln v)/dv = 1/v, so dv/v = d(ln v) d(ln v) = –k dx, which we can integrate to give ln v – ln v0 = – kx, where we have chosen the constant of integration – ln v0 so that v = v0 at x = 0. Taking antilogs of both sides and rearranging gives us
So a plot of ln(v/v0) vs x gives us k, provided we are in the high v region, where this plot is linear. How fast can a car go?Suppose that the road is flat, that a power P is transmitted to the wheels and that that power is used only to overcome rolling resistance and aerodynamic drag, so, using the equations above for power P and drag force Fdrag,
For solar cars, the power available depends on whether one uses batteries or not. However, for the solar car land speed record, batteries are not allowed: the power used must be supplied, in real time, only by the sun. In 2011, Sunswift set the Land Speed Record for solar cars. Yes, 88 kph on the power of a hair-dryer. But one final comment about car physics and speed: the risk of being in a serious collision doubles for every 5 kph above 60 kph. Please read this important page.
|
|
||||||||