Wheelstands or 'wheelies'

In Wheelstands or 'wheelies', if there is sufficient torque, the front wheels of a front wheels of a rear-drive car or bike can lift off the ground during forwards acceleration. What are the conditions of torque, friction, centre of mass and geometry under which they happen? In a very similar problem, we consider whether it is possible for a cyclist to brake so hard with the front wheel that s/he can rotate about the front axle and travel over the handlebars. In both cases, I urge readers not to try either of these experimentally, for obvious reasons. (And we can argue that, if I put some analysis and video here, it ought to make it less likely that readers will go and investigate experimentally.)

In the sketch, a vehicle accelerates towards the right. The centre of mass (CM) is a distance L ahead of the rear wheels, and a height H above the horizontal road. The front wheels have just left contact with the road, because the vehicle has rotated a little, but with negligible angular acceleration. The rear wheels are driven, so the contact force exerted on them by the road may be decomposed into a normal component N and a frictional component F_f, shown by the vector arrows. (For a revision, see Weight and Contact Forces.)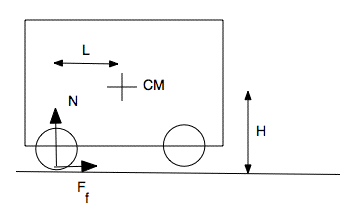



Consider rotation and torques acting about the centre of mass. (Why this point? See below*.) In the counter-clockwise direction, the friction exerts a positive torque HF_f and the normal force a torque − LN. If the angular acceleration is negligible, as assumed, then these add to zero, so

HF_f  =  LN
Because the rotation is slow, the centre of mass is not accelerating upwards rapidly, so the vertical forces add to zero. Let's neglect any positive or negative lift that might be generated (at high speed) by the body or spoilers. So, on a horizontal road, the normal force N equals the weight mg. Substituting and rearranging:
F_f  =  mgL/H
This equation gives us the:

Force and torque condition. The rear wheels must be capable of supplying a force of mgL/H. For a typical car, L is greater than H. For a bicycle, however, it could be less. However, it is of order unity, so the horizontal force supplied by the wheels must be comparable with the weight of the vehicle. The required torque, on a wheel with radius r, is of course  τ  =  rF_f  =  rmgL/H. With this force (or torque), the vehicle would accelerate forwards at F_f/m, so the wheelie would be produced during a forwards acceleration of gL/H.

Friction condition. An upper bound to the friction force F_f is imposed by limiting friction. With a coefficient of static friction μ_s, friction satisifies

F_f  ≤  μ_sN  =  μ_smg
Substituting for F_f from the force condition above gives this constraint: to perform the wheelie,
mgL/H  ≤  μ_smg,
which gives the geometrical constraint:
L/H  ≤  μ_s.

The coefficient of static friction μ_s is typically about 1, but could be as high as say 1.2 for a clean dry road. As mentioned above, for a typical car, L is greater than H, so such a (rear-drive) car would skid the rear wheels before the front wheels lifted off. For motor cycles (and some bicycles), however, L/H could be rather less than one. In the photo shown below, this ratio is no more than 1/5. So, with sufficient torque available by using low gears, the front wheel can be lifted off rather easily.

Slope. On a hill with slope θ, the torque exerted by the normal force is reduced by a factor cos θ, and the normal force is also less than mg. So it is easier to do a wheelie on a steep slope. The effect is not large on a road on public roads, because slopes are rarely more than several degrees, so the cos term is very close to unity. For a 10% slope, θ = 5.7° and cos θ = 0.995. For a 20% slope, θ = 11.5° and cos θ = 0.98.

Using a low gear on my bicycle to pedal up library hill at UNSW, I've accidentally lifted the front wheel. In the photo at right, I did it briefly and deliberately. (Warning: lifting a wheel is dangerous. Library hill is not a public road, and the slope is about 17% – much greater than a normal road, and it feels greater still.) Here, the wheel lifting is not directly due to the cos θ term, but rather a sin θ term: because the road is steep, I am pedalling hard, so F_f is large.

It's quite easy to this. I live in a very hilly area, and so have a very low gear of my bike: the smallest front sprocket and the largest back sprocket have the same diameter. Using this gear, the torque applied at the back wheel equals that appled by the pedals. (For normal gear ratios, where the rear sprocket is small, the torque on the wheel is rather less.) Now the radius r of the wheel is greater than the length R of the pedal crank so, in this low gear, the force applied to the ground by the tires is less than that applied at the pedals by a factor R/r, which is about 1/2. Standing on the pedals, one can exert a force of order mg, but it can be greater than this if one pulls up on the handle bars. So, in normal riding, F_f is rather less than mg/2. However, looking at this photo, we see that L/H is much less than 1/2, so it's quite relatively easy to lift the front wheel.

Hard braking

This is the same diagram as above, but now it represents a vehicle travelling to the left while braking so hard that the rear wheels lift off. (It is decelerating to the left, which is the same as accelerating to the right, so I can use the same diagram.) Of course, here L' measures the distance of the centre of mass behind the front wheels, which is not the same as L, the distance ahead of the rear wheels. (L and L' are probably fairly similar for many cars, but not for trucks, busses and cars designed for drag racing.)

In an extreme stop, for the rear wheels just to lift off, this time we have

L'/H  ≤  μ_s.

While this is unlikely to be satisified for a car, it is possible for a bicycle, particularly if the cyclist is leaning forwards over the handlebars, which makes L' small.

In the next photo, L'/H is about 1/2 and the coefficient of static friction would be a bit over one, so it is in principle possible to lift the back wheel, if the front brake can supply sufficient force. Should you therefore use the rear brake to stop? Using the rear brake is dangerous. First, in stopping, the tendency is to rotate forward, so there is less normal force on the rear wheel and so the rear wheel is likely to skid. (And, if you are approaching the condition of going over the handlebars, the back wheel has no normal force so there is no point using the back brake.) A rear-wheel skid is particularly dangerous because, when skidding, the rear wheel can travel sideways as well as forwards. So the rear wheels can then overtake the front wheels. For this reason, car makers put much bigger brakes on the front of cars than on the rear. A car is more likely to stop in a straight line if the front wheels skid than if the rear wheels skid.

This final pic is included for another reason. Everyone, and not just cyclists, tends to overestimate slopes. Looking down or up, or riding it, this slope seems seriously steep, and the first several people I asked all estimated it at more than 20% (1 in 5). The sideways pictures, however, tell us that it is about 17%, or 10°, for which cos θ is 0.984. So the slope is still not directly important in the tipping term! It is, however, indirectly important. Because the slope is steep I have to pedal hard going up and brake hard descending, so the sin θ term requires, in both cases, a large Ff. * This footnote is a complication I've put aside to discuss later – and later is now. The analysis of rotation given here is conducted about the centre of mass, which is of course accelerating in this case because of Ff. In general, Newton's laws don't apply in a non-inertial frame. In a frame accelerating at a, a fictitious force − ma appears to act on the centre of mass. If we considered rotation about any accelerating point other than the centre of mass, we should have to include the torque due to this fictitious force.

See also Car Physics