

 |

|
|
A Newtonian analysis of the black hole merger and its radiation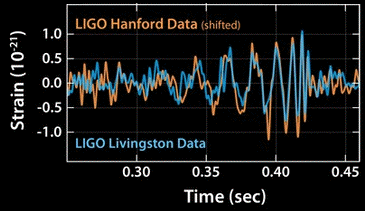
Black hole fusion was the biggest science story of 2016: the Large Interferometric Gravitational Observatory (LIGO) reported measurements of the gravity waves radiated by two black holes as they orbited about a point roughly midway between them, spiraling inwards and ultimately fusing together. They were 1.3 billion light-years away (1.3x1022 km) and each black hole was about 30 times the mass of the sun. LIGO has an animation of what it would have looked like close up. I was teaching first year mechanics at UNSW that year and the syllabus includes classical, Newtonian gravity. So we analysed different parts of this problem. Strictly, this is a very difficult problem in general relativity. We used only Newtonian mechanics, but this gives a quite simple answer that is, surprisingly, not wildly wrong.
What does the famous graph mean?To simplify, the LIGO team measured changes in the lengths of the arms of two interferometers (length 4 km) as a function of time: the graph covers 0.2 seconds of the record. Here they plot the fractional change in length (that's what strain means). The vertical range goes from about −10−21 to +10−21. Plus or minus 0.000 000 000 000 000 000 1%. This very tiny change is due not to vibration* of the ground (as we can see by comparing the signals from two different interferometers located thousands of km apart, shown as different colours on the graph). Rather, it is from the contraction and expansion of space itself as the wave goes by, because that's what gravity waves do. Note that the signal is noisy at first, then, when a clear oscillation begins, it increases in both amplitude and frequency until, at about 0.43 seconds, it suddenly disappears into the background. The increase in frequency and amplitude are both explained by the orbits becoming smaller and faster until the black holes fused. As these objects fell towards each other, they lost gravitational potential energy, converting part of it into kinetic energy (going faster) and the rest into gravitational radiation that spread out and, a billion or so years later, went past and through the earth. *One could say that the LIGO team measured the 'time of flight' for photons, which partly answers the anticipated question about whether the wavelength and space shrink by the same fraction. By the way, one member of the very large LIGO team and thus one of the many authors on the paper reporting it was Ra Inta, a PhD graduate from our Acoustics Lab. In our lab, he studied how to produce vibration, now his job is to avoid vibration. The paper is Abbott, B.P. et al. (LIGO Scientific Collaboration and Virgo Collaboration). Phys. Rev. Lett. 116, 061102 (2016). What is a black hole?
"What goes up, must come down" sang Blood, Sweat and Tears, but Isaac Newton was probably the first person to know that this isn't necessarily true. If you give an object enough speed (the definition of escape speed ve) at the surface of the earth/star/etc, it will escape from that object's gravitational field. To derive it, see Newton's law of universal gravitation. But briefly: the gravitational force between masses M and m at radial separation of centres r is −GMm/r2 , where G is Newton's constant and the minus sign means it's attractive. We integrate the negative of this force over r to derive the potential energy U of a mass m, at distance r from the centre of a planet/etc of mass M as U = −GMm/r. If we move m from the object's surface at radius R to a very long way away (the latter is taken as the zero of potential energy), we have to gain potential energy GMm/R. If we start with escape speed ve and therefore kinetic energy ½mve2 and come almost to rest a long way away, we lose that kinetic energy. In space, without friction or air, the loss of kinetic energy equals the gain in potential energy and we reorganise the equation to have ve = (2GM/R)½. For the earth, the escape speed is about 11 km per second, or about 30 times the speed of sound. But the equation above tells us that escape speed increases for massive planets or stars and for small radii. So, for very dense objects (big M, small R), the escape speed can reach the speed of light. If an object has this high ratio of M/R, then even light cannot escape: it's a black hole. Rearranging the equation above for ve, and using the speed of light c as the escape speed, the radius of a black hole of mass M is R = 2GM/c2. Now c is very big and G is very small, so R is small. If we compressed the earth to a diameter of 18 mm or the sun to 6 km, they would be black holes. (Neither is likely to happen.) By the way, this calculation was first made by John Mitchell in 1783. He called such objects 'dark stars' – a bit more romantic than black holes. And, thanks to some fortuitous cancellation of errors, this is exactly the result that comes from the correct calculation using General Relativity. This gives us hope that, when we neglect relativistic effects below, we'll still get an order-of-magnitude estimate. How big were these black holes and why did they fuse?The homework challenge to the class was to explain why the wiggles in the graph stop when the frequency goes above about 200 Hz. What? Yes, these gigantic dark stars were orbiting the midpoint between them at rates increasing to about 100 times per second and above. If this hasn't shocked you, imagine a planet whose 'year', i.e. its orbital period, was 0.01 seconds. (Think of all the birthday gifts you'd have to buy!) These black holes were vibrating space at about twice the orbital frequency (because there are two objects in each orbit), and thus at frequencies of up to 100 Hz or so. So the challenge question to the first years included relating the (classical, constant) orbital radius to the black hole radius. LIGO tells us that each had a mass of about 30 times that of the sun so, using the relation above, they have a diameter of about 30 km. It's easy enough to make a rough estimate of the diameter D of their orbit, if we assume it's circular and forget about the fact that it's shrinking. Here, we use Newton's 1st and 2nd law F = ma. For the force, use gravity: F = −GM2/D2 (their separation is one diameter D of the orbit); for the acceleration in circular motion, a = (D/2)(2πf)2. Combining these to obtain D, we see that they begin to fuse when the separation is not much larger than the black hole radius. Of course, they are spiralling, so the orbits are no longer circular, but this analysis is just to give a rough estimate. How powerful was the radiation? Once again, if we're prepared to pretend this is a classical problem, we can get an estimate from the energies of the orbit. Again pretending that it's a circular orbit, we know its energy. The potential energy is just U = −GMm/D, as above. We can get the kinetic energy by setting (as above) gravitational attraction equal to mass times centripetal acceleration. The kinetic energy is therefore GMm/2D, which gives us the total energy E = −GMm/2D. (And in our problem, we're making the approximation that the two black holes have roughly equal mass: m = M.) Then we can look at the graph above to quantify the variation in the orbital period just before it fuses. It looks as though the energy goes from E/2 down to E in something like 10 ms. (Both E/2 and E are negative, so they are losing energy, going from high, slow orbit to low, fast orbit, like a satellite spiralling down in Earth orbit. Kepler's law of periods has T2 ∝ D3. We had above that −E ∝ 1/D; combining these gives −E ∝ 1/T2/3.) Where is that lost orbital energy going? For the black holes, nearly all of it went into gravitational radiation. And so we can estimate the power output of the source: it's just −E/2 in time 10 ms. That simple calculation gives a power of several times 1049 W. Now that 49 in the exponent perhaps doesn’t look sufficiently impressive. So the last question for the students was this: our sun radiates 4x1026 W (mainly in visible light). There are about a hundred billion stars in a typical galaxy, and about a hundred billion galaxies in the visible universe. How does their output compare with the power of these gravitational waves (in the last 10 ms or so before fusion) with the power emitted by all the stars in the observable universe: (4x1026 W per star) times (1011 stars per galaxy) times 1011 galaxies gives 4x1048 W. So the power of the gravitational radiation from that event was, briefly, more powerful than the electromagnetic radiation from all the stars in all the galaxies of the visible universe. (As one student wrote: "either I can't calculate or this is amazing".) But this raises an interesting question: if it was that powerful, why didn't we hear it? (A colleague and I wrote an essay about this for Nature Physics.) (By the way, it wouldn't sound like a chirp of rising pitch: the frequency varies too rapidly for us to hear a pitch. Rather, it would sound like a click.) Of course it was a long away (1.3 billion light-years, or 1.3x1025 m). But even so, dividing the power by 4π*Distance2 to get the power per unit area, the intensity received here in the Milky Way was roughly 0.02 watts per square metre. Which is not all that small: light intensity at this level is brighter than full moon on a clear night Or, for another comparison, sound at this intensity is fairly loud: it's 103 decibels. So hey, these waves were distorting our heads, including our ears: could we have heard them? No, obviously enough, or it wouldn't have taken such a huge effort to detect them.
Gravity is a very weak force: for an electron and a proton, gravitational attraction is about 1039 times weaker than electrical. One might say that gravity interacts only weakly with mass and with space. Consequently, even when the waves have considerable intensity, the resultant distortion of space is minuscule. Which raises the question: if gravity is so weak, why does it create and move stars and galaxies? The answer here is simple: electric charge comes in positive and negative forms, but there is no negative mass. Every object you can see contains a number of protons (positive charge) and electrons (negative) that are extremely close to being equal. So electricity almost exactly cancels out for macroscopic objects. But gravity never cancels out (unless you count dark energy as cancellation). I'm made of several times 1028 protons and the same number of electrons (and, because most of my atoms are hydrogen, rather fewer neutrons, which are uncharged). If I lost 1% of my electrons, I'd have a charge of several hundred kilocoulombs. This would charge me up to about V = q/C ~ qr/4πε0 ~ 1015 volts and I'd explode spectacularly from the electrostatic repulsion. So, in an important sense, the answer to this question is not because space doesn't transmit sound well, and it's not that the signal was weak. Rather, it's that it was the wrong sort of signal and it went right through us with no effect. Or, if you like, because gravity is very weak. But my comparison of the strength of gravity and electricity was rather arbitrary, in that I chose electrons and protons. (What else to chose? If I'd chosen neutrons or dark matter then there'd be no electromagnetic forces and also no EM radiation!) It’s tempting to say, simplistically, that space is much ‘stiffer’ than air (or water etc.) — as suggested by the faster wave speed. But gravity (a gauge wave) and sound (a Goldstone wave) are qualitatively different types of waves. Expressed independently of frequency or wavelength, sound intensity goes as strain squared (vsoundκε2), whereas gravitational wave intensity goes as the square of its derivative ((c5/8πG)(∇ε)2or (c3/8πG)(∂ε/∂t)2 whence (πc3/2G)f2ε2), where symbols have their usual meaning. Comparing these expressions, the ‘stiffness’ of space (its analogy of adiabatic modulus κ) is (πc)2f2/2G. And looking at the dependence on c, f and G, we'd say that space is stiff indeed — in terms of everyday units. It would be nice to have a non-dimensional comparison. But we can’t really compare the stiffness of space for different forces: not all objects accelerate at the same rate in an electric field, for example, so we can’t readily describe other forces with geometrical theories analogous to general relativity. Finally, the bulk modulus κ and density ρ of matter depend ultimately on the quantum mechanics of its atoms and their interactions, whereas general relativity is universal and — at least to our current knowledge — unrelated to quantum mechanics. (We used this argument in a little paper in Nature Physics.) Why is this discovery so important? One reason physicists are excited about this result is because, in principle, gravity might give us important information not only about cataclysmic events like this one, but about the very early universe. The universe only became transparent when it was about 300,000 years old: before that, all of the atoms were ionised – the universe was a plasma (a lightning flash is a familiar example of a plasma). So our radio (and optical) telescopes can only look back to that time: radiation from that period, now cooled from several thousands of kelvins to 3 kelvins (or -270°C), are what we see in the famous pictures from the COBE and WMAP satellites. In principle, gravity waves and neutrinos can bring us direct information from much hotter, earlier times.
This is a supporting page to the multimedia tutorial on gravitation in Physclips. |
|
||||||||