Sound pressure, sound level and dB. Sound is usually measured with microphones and they respond proportionally to the sound pressure, p. Now the power in a sound wave, all else equal, goes as the square of the pressure. (Similarly, electrical power in a resistor goes as the square of the voltage.) The log of x² is just 2 log x, so this introduces a factor of 2 when we convert pressure ratios to decibels. The difference in sound pressure level between two sounds with p₁ and p₂ is therefore:

20 log (p₂/p₁) dB   =  10 log (p₂²/p₁²) dB   = 10 log (P₂/P₁) dB       (throughout, the log is to base 10).

What happens when you halve the sound power? The log of 2 is 0.3010, so the log of 1/2 is -0.3, to a good approximation. So, if you halve the power, you reduce the power and the sound level by 3 dB. Halve it again (down to 1/4 of the original power) and you reduce the level by another 3 dB. If you keep on halving the power, you have these ratios.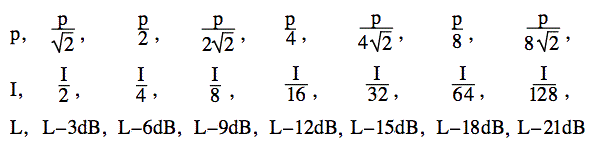

What happens if I add two identical sounds? Do I double the intensity (increase of 3 dB)? Or do I double the pressure (increase of 6 dB)? This frequently asked question is a little subtle, so it is discussed here on our FAQ.

Sound files to show the size of a decibel

We saw above that halving the power reduces the sound pressure by √2 and the sound level by 3 dB. That is what we have done in the first graphic and sound file below.

The first sample of sound is white noise (a mix of a broad range of audible frequencies, analogous to white light, which is a mix of all visible frequencies). The second sample is the same noise, with the voltage reduced by a factor of √2. Now 1/√2 is approximately 0.7, so -3 dB corresponds to reducing the voltage or the pressure to 70% of its original value. The green line shows the voltage as a function of time. The red line shows a continuous exponential decay with time. Note that the voltage falls by 50% for every second sample. Note, too, that a doubling of the power does not make a huge difference to the loudness. We'll discuss this further below, but it's a useful thing to remember when choosing sound reproduction equipment. Sound files and animation by John Tann and George Hatsidimitris. Sorry, animation doesn't run on Safari.

How big is a decibel? In the next series, successive samples are reduced by just one decibel.

One decibel is of the same order as the Just Noticeable Difference (JND) for sound level. As you listen to these files, you will notice that the last is quieter than the first, but it is rather less clear to the ear that the second of any pair is quieter than its predecessor. 10*log10(1.26) = 1, so to increase the sound level by 1 dB, the power must be increased by 26%, or the voltage by 12%.

What if the difference is less than a decibel? Sound levels are rarely given with decimal places. The reason is that sound levels that differ by less than 1 dB are hard to distinguish, as the next example shows. (This makes the dB a convenient size unit.)

0.3 dB steps. You may notice that the last is quieter than the first, but it is difficult to notice the difference between successive pairs. 10*log10(1.07) = 0.3, so to increase the sound level by 0.3 dB, the power must be increased by 7%, or the voltage by 3.5%.

Standard reference levels ('absolute' sound level)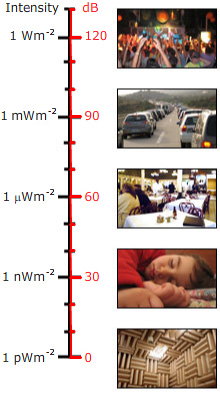

We said above that the decibel is a ratio. So, when it is used to give the sound level for a single sound rather than a ratio, a reference level must be chosen. For sound pressure level, the reference level (for air) is usually chosen as p_ref = 20 micropascals (20 μPa), or 0.02 mPa. This is very low: it is 2 ten billionths of an atmosphere. Nevertheless, this is about the limit of sensitivity of the human ear, in its sensitive range of frequency. (Usually this sensitivity is only found in rather young people or in people who have not been exposed to loud music or other loud noises. Personal music systems with in-ear speakers are capable of very high sound levels in the ear, and are believed by some to be responsible for much of the hearing loss in young adults in some countries.)

So if you read of a sound pressure level of 86 dB, it means that

20 log (p₂/p_ref) = 86 dB

where p_ref is the sound pressure of the reference level, and p₂ that of the sound in question. Divide both sides by 20:

log (p₂/p_ref) = 4.3

p₂/p_ref = 10^4.3

4 is the log of 10 thousand, 0.3 is the log of 2, so this sound has a sound pressure 20 thousand times greater than that of the reference level (p₂/p_ref = 20,000) or an intensity 400 million times the reference intensity. 86 dB is a loud sound but not dangerous—provided that exposure is brief.

What does 0 dB mean? This level occurs when the measured intensity is equal to the reference level. i.e., it is the sound level corresponding to 0.02 mPa. In this case we have

sound level = 20 log (p_measured/p_ref) = 20 log 1 = 0 dB

Remember that decibels measure a ratio. 0 dB occurs when you take the log of a ratio of 1 (log 1 = 0). So 0 dB does not mean no sound, it means a sound level where the sound pressure is equal to that of the reference level. This is a small pressure, but not zero. It is also possible to have negative sound levels: - 20 dB would mean a sound with pressure 10 times smaller than the reference pressure, i.e. 2 μPa.

Not all sound pressures are equally loud. This is because the human ear does not respond equally to all frequencies: we are much more sensitive to sounds in the frequency range about 1 kHz to 7 kHz (1000 to 7000 vibrations per second) than to very low or high frequency sounds. For this reason, sound meters are usually fitted with a filter whose response to frequency is a bit like that of the human ear. (More about these filters below.) If the "A weighting filter" is used, the sound pressure level is given in units of dB(A) or dBA. Sound pressure level on the dBA scale is easy to measure and is therefore widely used. One reason why it is different from loudness is because the filter does not respond in the same way as the ear. To understand the loudness of a sound, the first thing you need to do consult some curves representing the frequency response of the human ear, given below. (Alternatively, you can measure your own hearing response.) Another reason is that human hearing is not logarithmic.

Logarithmic measures

Why do we use decibels? The ear is capable of hearing a very large range of sounds: the ratio of the sound pressure that causes permanent damage from short exposure to the limit that (undamaged) ears can hear is more than a million. To deal with such a range, logarithmic units are useful: the log of a million is 6, so this ratio represents a difference of 120 dB. Hearing is not inherently logarithmic in response. (Logarithmic measures are also useful when a sound (briefly) increases or decreases exponentially over time. This happens in many applications involving proportional gain or proportional loss.)

The filters used for dBA and dB(C)

The most widely used sound level filter is the A scale, which roughly corresponds roughly to the inverse of the 40 dB (at 1 kHz) equal-loudness curve. Using this filter, the sound level meter is thus less sensitive to very high and very low frequencies. Measurements made on this scale are expressed as dBA. The C scale varies little over several octaves and is thus suitable for subjective measurements only for moderate to high sound levels. Measurements made on this scale are expressed as dB(C). There is also a (rarely used) B weighting scale, intermediate between A and C. The figure below shows the response of the A filter (left) and C filter, with gains in dB given with respect to 1 kHz. (For an introduction to filters, see RC filters, integrators and differentiators.)



On the music acoustics and speech acoustics sites, we plot the sound spectra in dB. The reason for this common practice is that the range of measured sound pressures is large.

dB(G) measurements use a narrow band filter that gives high weighting to frequencies between 1 and 20 Hz, and low weighting to others. It thus gives large values for sounds and infrasounds that cannot readily be heard. ISO 7196:1995

Loudness, phons and sones, hearing response curves

The phon is a unit that is related to dB by the psychophysically measured frequency response of the ear. At 1 kHz, readings in phons and dB are, by definition, the same. For all other frequencies, the phon scale is determined by the results of experiments in which volunteers were asked to adjust the loudness of a signal at a given frequency until they judged its loudness to equal that of a 1 kHz signal. To convert from dB to phons, you need a graph of such results. Such a graph depends on sound level: it becomes flatter at high sound levels.


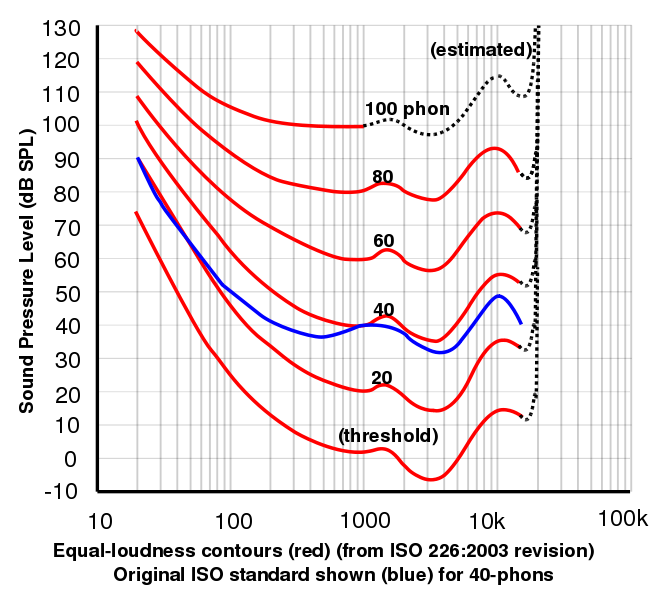This graph, courtesy of Lindosland, shows the 2003 data from the International Standards Organisation for curves of equal loudness determined experimentally. Plots of equal loudness as a function of frequency are often generically called Fletcher-Munson curves after the original work by Fletcher, H. and Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. You can make your own curves using our hearing response site.

The sone is derived from psychophysical measurements which involved volunteers adjusting sounds until they judge them to be twice as loud. This allows one to relate perceived loudness to phons. One sone is defined to be equal to 40 phons. Experimentally it was found that, above 40 phons, a 10 dB increase in sound level corresponds approximately to a perceived doubling of loudness. So that approximation is used in the definition of the sone: 1 sone = 40 phon, 2 sone = 50 phon, 4 sone = 60 phon, etc.



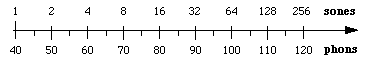
This relation implies that loudness and intensity are related by a power law: loudness in sones is proportional to (intensity)^log 2 = (intensity)^0.3.

Wouldn't it be great to be able to convert from dB (which can be measured by an instrument) to sones (which approximate loudness as perceived by people)? This is sometimes done using tables that you can find in acoustics handbooks. However, if you don't mind a rather crude approximation, you can say that the A weighting curve approximates the human frequency response at low to moderate sound levels, so dB(A) is very roughly the same as phons, over a limited range of low levels. Then one can use the logarithmic relation between sones and phons described above.

Recording level and decibels

Meters measuring recording or output level on audio electronic gear (mixing consoles etc) are almost always recording the AC rms voltage (see links to find out about AC and rms). For a given resistor R, the power P is V²/R, so
difference in voltage level = 20 log (V₂/V₁) dB   =  10 log (V₂²/V₁²) dB   = 10 log (P₂/P₁) dB,    or

absolute voltage level = 20 log (V/V_ref)

where V_ref is a reference voltage. So what is the reference voltage?

The obvious level to choose is one volt rms, and in this case the level is written as dBV. This is rational, and also convenient with analog-digital cards whose maximum range is often about one volt rms. So one has to remember to the keep the level in negative dBV (less than one volt) to avoid clipping the peaks of the signal, but not too negative (so your signal is still much bigger than the background noise).

Sometimes you will see dBm. This used to mean decibels of electrical power, with respect to one milliwatt, and sometimes it still does. However, it's complicated for historical reasons. In the mid twentieth century, many audio lines had a nominal impedance of 600 Ω. If the impedance is purely resisitive, and if you set V²/600  Ω = 1 mW, then you get V = 0.775 volts. So, providing you were using a 600  Ω load, 1 mW of power was 0 dBm, which was 0.775 V, so you calibrated your level meters thus. The problem arose because, once a level meter that measures voltage is calibrated like this, it will read 0 dBm at 0.775 V even if it is not connected to 600  Ω So, perhaps illogically, dBm will sometimes mean dB with respect to 0.775 V. (When I was a boy, calculators were expensive so I used dad's old slide rule, which had the factor 0.775 marked on the cursor window to facilitate such calculations.)

How to convert dBV or dBm into dB of sound level? There is no simple way. It depends on how you convert the electrical power into sound power. Even if your electrical signal is connected directly to a loudspeaker, the conversion will depend on the efficiency and impedance of your loudspeaker. And of course there may be a power amplifier, and various acoustic complications between where you measure the dBV on the mixing desk and where your ears are in the sound field.

Intensity, radiation and dB

How does sound level (or radio signal level, etc) depend on distance from the source? A source that emits radiation equally in all directions is called isotropic. Consider an isolated source of sound, far from any reflecting surfaces – perhaps a bird singing high in the air. Imagine a sphere with radius r, centred on the source. The source outputs a total power P, continuously. This sound power spreads out and is passing through the surface of the sphere. If the source is isotropic, the intensity I is the same everywhere on this surface, by definition. The intensity I is defined as the power per unit area. The surface area of the sphere is 4πr2, so the power (in our example, the sound power) passing through each square metre of surface is, by definition: I = P/4πr2. So we see that, for an isotropic source, intensity is inversely proportional to the square of the distance away from the source: I2/I1 = r12/r22. But intensity is proportional to the square of the sound pressure, so we could equally write: p2/p1 = r1/r2. So, if we double the distance, we reduce the sound pressure by a factor of 2 and the intensity by a factor of 4: in other words, we reduce the sound level by 6 dB. If we increase r by a factor of 10, we decrease the level by 20 dB, etc. Be warned, however, that many sources are not isotropic, especially if the wavelength is smaller than, or of a size comparable with the source. Further, reflections are often quite important, especially if the ground is nearby, or if you are indoors.

Pressure, intensity and specific impedance

For acoustic waves, the specific acoustic impedance z is defined as the ratio of the acoustic pressure p to the average particle velocity u, due to the sound ave,   z  =  p/u  . In Acoustic impedance, intensity and power, we show how to relate RMS acoustic pressure p and intensity I:
I  =  p²/z
For air, the specific acoustic impedance z is 420 kg.s⁻¹.m⁻²  =  420 Pa.s.m⁻¹. For (fresh) water, the specific acoustic impedance for water is 1.48 MPa.s.m⁻¹. So a sound wave in water with the same pressure has a much lower intensity than one in air.

dBi and radiation that varies with direction

Radiation that varies in direction is called anisotropic. For many cases in communication, isotropic radiation is wasteful: why emit a substantial fraction of power upwards if the receiver is, like you, relatively close to ground level. For sound of short wavelength (including most of the important range for speech), a megaphone can help make your voice more anisotropic. For radio, a wide range of designs allows antennae to be highly anisotropic for both transmission and reception.

So, when you interested in emission in (or reception from) a particular direction, you want the ratio of intensity measured in that direction, at a given distance, to be higher than that measured at the same distance from an isotropic radiator (or received by an isotropic receiver). This ratio is called the gain; express the ratio in dB and you have the gain in dBi for that radiator. This unit is mainly used for antennae, either transmitting and receiving, but it is sometimes used for sound sources and directional microphones.

Example problems

A few people have written asking for examples in using dB in calculations. So...
• All else equal, how much louder is loudspeaker driven (in its linear range) by a 100 W amplifier than by a 10 W amplifier?

  The powers differ by a factor of ten, which, as we saw above, is 10 dB. All else equal here means that the frequency responses are equal and that the same input signal is used, etc. So the frequency dependence should be the same. 10 dB corresponds to 10 phons. To get a perceived doubling of loudness, you need an increase of 10 phons. So the speaker driven by the 100 W amplifier is twice as loud as when driven by the 10 W, assuming you stay in the linear range and don't distort or destroy the speaker. (The 100 W amplifier produces twice as many sones as does the 10 W.)

• I am standing at a distance R from a small source of sound (size much less than R), at ground level out in the open where reflections may be neglected. The sound level is L. If I now move to a distance nR (n a number, and nR still much greater than the size of the source), what will be the new sound level?

  First, note that the neglect of reflections is very important. This calculation will not work inside a room, where reflections from the wall (collectively producing reverberation) make the calculation quite difficult. Out in the open, the sound intensity is proportional to 1/r², where r is the distance from the source. (The constant of proportionality depends on how well the ground reflects, and doesn't concern us here, because it will roughly cancel in the calculation, provided r is reasonably large.) So, if we increase r from R to nR, we decrease the intensity from I to I/n ².

  The difference in decibels between the two signals of intensity I ₂ and I ₁ is defined above to be

   ΔL = 10 log (I₂/I₁) = 10 log ((I/n ²)/I) = 10 log (1/n ²) = −10 log (n ²) = −20 log n.

  For example, if n is 2 (ie if we go twice as far away), the intensity is reduced by a factor of four and sound level falls from L to (L − 6dB).

• If, in ideal quiet conditions, a young person can hear a 1 kHz tone at 0 dB emitted by a loudspeaker (perhaps a softspeaker?), by how much must the power of the loudspeaker be increased to raise the sound to 110 dB (a dangerously loud but survivable level)?

  The difference in decibels between the two signals of power P₂ and P₁ is defined above to be

   ΔL = 10 log (P₂/P₁) dB   so, raising 10 to the power of these two equal quantities:
  10^L/10 = P₂/P₁   so:
  P₂/P₁ = 10^110/10 = 10¹¹  = one hundred thousand million.
  which is a demonstration that the human ear has a remarkably large dynamic range, perhaps greater than that of the eye.

• An amplifier has an input of 10 mV and and output of 2 V. What is its voltage gain in dB?

  Voltage, like pressure, appears squared in expressions for power or intensity. (The power dissipated in a resistor R is V²/R.) So, by convention, we define:

  gain = 20 log (V_out/V_in)
       = 20 log  (2V/10mV)
       = 46 dB

  (In the acoustic cases given above, we saw that the pressure ratio, expressed in dB, was the same as the power ratio: that was the reason for the factor 20 when defining dB for pressure. It is worth noting that, in the voltage gain example, the power gain of the ampifier is unlikely to equal the voltage gain, which is defined by the convention used here. The power is proportional to the square of the voltage in a given resistor. However, the input and output impedances of amplifiers are often quite different. For instance, a buffer amplifier or emitter follower has a voltage gain of about 1, but a large current gain.)

• What is the difference, in dB, between the irradiance (light intensity) on earth (8.3 light minutes from the sun) and on Uranus (160 light minutes)?

  Like sound, isotropic light intensity decreases as r⁻², so the intensity ratio is (160/8.3)² = 20 log (160/8.3) = 26 dB.

Occupational health and safety

Different countries and provinces obviously have different laws concerning noise exposure at work, which are enforced with differing enthusiasm. Many such regulations have a limit for exposure to continuous noise of 85 dB(A), for an 8 hour shift. For each 3 dB increase, the allowed exposure is halved. So, if you work in a nightclub where amplified music produces 100 dB(A) near your ears, the allowed exposure is 15 minutes. There is a limit for impulse noise like firearms or tools that use explosive shots. (e.g. 140 dB peak should not be exceeded at any time during the day.) There are many documents providing advice on how to reduce noise exposure at the source (ie turn the music level down), between the source and the ear (ie move away from the loudspeakers at a concert) and at the ear (ie wear ear plugs or industrial hearing protectors). Noise management and protection of hearing at work is the code of practice in the state of New South Wales, Australia (the author's address).

Some FAQs

• How loud is an aircraft? A train? A person singing? A dog barking? A power tool? The answers to this question vary considerably. It depends strongly upon how far away you are, whether you are indoors or not, whether there is reverberation, how strong the particular source is and what its spectrum is. To give values, without being very specific about the conditions, would be somewhat misleading. Because the rest of this page is intended to be reliable, as far as it goes, I'd rather not give values here.

• How does one "add decibels"?, meaning What sound level do you get when you add level a to level b? If the sources are coherent (which usually means that they ultimately come from the same source), then there may be complicated interference effects. In most cases, where the sources are independent, one can add the intensities and then convert to decibels. However, if you are given the sound levels in dB(A), it is not so easy to go back to intensity, and one must know something about the spectrum of the sound. If you know the distribution of the sound in different frequency bands, you can use the applet on this link.

• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?
  • How loud is the fusion of two black holes? (A colleague and I wrote a little paper about this for Nature Physics.)

---

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
  
• FAQ in music acoustics
  
• Loudness and spectra: how spectral content and other features are related to loudness
  
• Formants: what are they? A discussion of the different meanings of this term
  
• Music acoustics home page
  
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.
  

Physclips Home Site map for supporting pages The Australian Office for Learning and Teaching © School of Physics - UNSW 2052 Disclaimer Feedback
	This work is licensed under a Creative Commons License.