Some terminologyFor brevity, we shall refer to electrical potential difference as voltage. Throughout this page, we shall consider voltages and currents that vary sinusoidally with time. We shall use lower case v and i for the voltage and current when we are considering their variation with time explicitly. The amplitude or peak value of the sinusoidal variation we shall represent by Vm and Im, and we shall use V = Vm/√2 and I = Im/√2 without subscripts to refer to the RMS values. For an explanation of RMS values, see Power and RMS values. For the origin of the sinusoidally varying voltage in the mains supply, see Motors and generators.So for instance, we shall write:
i = i(t) = Im sin (ωt).
Resistors and Ohm's law in AC circuitsThe voltage v across a resistor is proportional to the current i travelling through it. (See the page on drift velocity and Ohm's law.) Further, this is true at all times: v = Ri. So, if the current in a resistor is
v = R.i = R.Im sin (ωt) v = Vm. sin (ωt) where Vm = R.Im So for a resistor, the peak value of voltage is R times the peak value of current. Further, they are in phase: when the current is a maximum, the voltage is also a maximum. (Mathematically, φ = 0.) The first animation shows the voltage and current in a resistor as a function of time.
The rotating lines in the right hand part of the animation are a very simple case of a phasor diagram (named, I suppose, because it is a vector representation of phase). With respect to the x and y axes, radial vectors or phasors representing the current and the voltage across the resistance rotate with angular velocity ω. The lengths of these phasors represent the peak current Im and voltage Vm. The y components are Im sin (ωt) = i(t) and voltage Vm sin (ωt)= v(t). You can compare i(t) and v(t) in the animation with the vertical components of the phasors. The animation and phasor diagram here are simple, but they will become more useful when we consider components with different phases and with frequency dependent behaviour. (To see where this rotating phasor idea comes from, see the comparison of simple harmonic motion and circular motion in Physclips.) What are impedance and reactance?Circuits in which current is proportional to voltage are called linear circuits. (As soon as one inserts diodes and transistors, circuits cease to be linear, but that's another story.) The ratio of voltage to current in a resistor is its resistance. Resistance does not depend on frequency, and in resistors the two are in phase, as we have seen above. However, circuits with only resistors are not very interesting.In general, the ratio of voltage to current does depend on frequency and in general there is a phase difference. So impedance is the general name we give to the ratio of voltage to current. It has the symbol Z. Resistance is a special case of impedance. Another special case is that in which the voltage and current are out of phase by 90°: this is an important case because when this happens, no power is lost in the circuit. In this case where the voltage and current are out of phase by 90°, the ratio of voltage to current is called the reactance, and it has the symbol X. We return to summarise these terms and give expressions for them below in the section Impedance of components, but first let us see why there are frequency dependence and phase shifts for capacitors and for inductors.
Capacitors and chargingThe voltage on a capacitor depends on the amount of charge you store on its plates. The current flowing onto the positive capacitor plate (equal to that flowing off the negative plate) is by definition the rate at which charge is being stored. So the charge Q on the capacitor equals the integral of the current with respect to time. From the definition of the capacitance,
Once again we have a sinusoidal current i = Im . sin (ωt), so integration gives
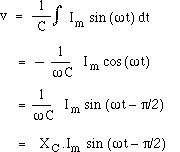
(The constant of integration has been set to zero so that the average charge on the capacitor is 0). Now we define the capacitive reactance XC as the ratio of the magnitude of the voltage to magnitude of the current in a capacitor. From the equation above, we see that XC = 1/ωC. Now we can rewrite the equation above to make it look like Ohm's law. The voltage is proportional to the current, and the peak voltage and current are related by
Note the two important differences. First, there is a difference in phase: the integral of the sinusoidal current is a negative cos function: it reaches its maximum (the capacitor has maximum charge) when the current has just finished flowing forwards and is about to start flowing backwards. Run the animation again to make this clear. Looking at the relative phase, the voltage across the capacitor is 90°, or one quarter cycle, behind the current. We can see also see how the φ = 90° phase difference affects the phasor diagrams at right. Again, the vertical component of a phasor arrow represents the instantaneous value of its quanitity. The phasors are rotating counter clockwise (the positive direction) so the phasor representing VC is 90° behind the current (90° clockwise from it). Recall that reactance is the name for the ratio of voltage to current when they differ in phase by 90°. (If they are in phase, the ratio is called resistance.) Another difference between reactance and resistance is that the reactance is frequency dependent. From the algebra above, we see that the capacitive reactance XC decreases with frequency . This is shown in the next animation: when the frequency is halved but the current amplitude kept constant, the capacitor has twice as long to charge up, so it generates twice the potential difference. The blue shading shows q, the integral under the current curve (light for positive, dark for negative). The second and fourth curves show VC = q/C . See how the lower frequency leads to a larger charge (bigger shaded area before changing sign) and therefore a larger VC.
Thus for a capacitor, the ratio of voltage to current decreases with frequency. We shall see later how this can be used for filtering different frequencies.
Inductors and the Farady emfAn inductor is usually a coil of wire. In an ideal inductor, the resistance of this wire is negligibile, as is its capacitance. The voltage that appears across an inductor is due to its own magnetic field and Faraday's law of electromagnetic induction. The current i(t) in the coil sets up a magnetic field, whose magnetic flux φB is proportional to the field strength, which is proportional to the current flowing. (Do not confuse the phase φ with the flux φB.) So we define the (self) inductance of the coil thus:
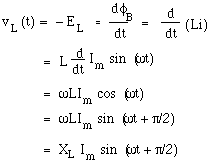
Again we define the inductive reactance XL as the ratio of the magnitudes of the voltage and current, and from the equation above we see that XL = ωL. Again we note the analogy to Ohm's law: the voltage is proportional to the current, and the peak voltage and currents are related by
Remembering that the derivative is the local slope of the curve (the purple line), we can see in the next animation why voltage and current are out of phase in an inductor.
Again, there is a difference in phase: the derivative of the sinusoidal current is a cos function: it has its maximum (largest voltage across the inductor) when the current is changing most rapidly, which is when the current is intantaneously zero. The animation should make this clear. The voltage across the ideal inductor is 90° ahead of the current, (ie it reaches its peak one quarter cycle before the current does). Note how this is represented on the phasor diagram. Again we note that the reactance is frequency dependent: XL = ωL. This is shown in the next animation: when the frequency is halved but the current amplitude kept constant, the current is varying only half as quickly, so its derivative is half as great, as is the Faraday emf. For an inductor, the ratio of voltage to current increases with frequency, as the next animation shows.
Impedance of componentsLet's recap what we now know about voltage and curent in linear components. The impedance is the general term for the ratio of voltage to current. Resistance is the special case of impedance when φ = 0, reactance the special case when φ = ± 90°. The table below summarises the impedance of the different components. It is easy to remember that the voltage on the capacitor is behind the current, because the charge doesn't build up until after the current has been flowing for a while.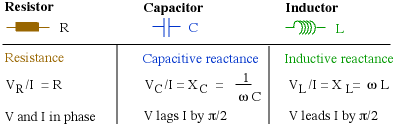
The same information is given graphically below. It is easy to remember the frequency dependence by thinking of the DC (zero frequency) behaviour: at DC, an inductance is a short circuit (a piece of wire) so its impedance is zero. At DC, a capacitor is an open circuit, as its circuit diagram shows, so its impedance goes to infinity. 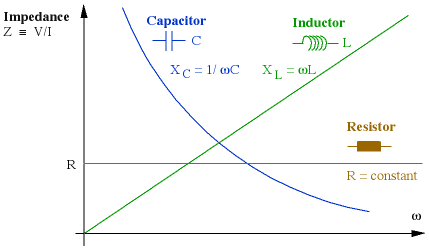
RC Series combinationsWhen we connect components together, Kirchoff's laws apply at any instant. So the voltage v(t) across a resistor and capacitor in series is just
Vseries < VR + VC.
Here's where phasor diagrams are going to save us a lot of work. Play the animation again (click play), and look at the projections on the vertical axis. Because we have sinusoidal variation in time, the vertical component (magnitude times the sine of the angle it makes with the x axis) gives us v(t). But the y components of different vectors, and therefore phasors, add up simply. Using bold for vectors or phasors: if
ry total = ry1 + ry2. Now let's stop that animation and label the values, which we do in the still figure below. All of the variables (i, vR, vC, vseries) have the same frequency f and the same angular frequency ω, so their phasors rotate together, with the same relative phases. So we can 'freeze' it in time at any instant to do the analysis. The convention I use is that the x axis is the reference direction, and the reference is whatever is common in the circuit. In this series circuit, the current is common. (In a completely parallel circuit, the voltage is common, so I would make the voltage the horizontal axis.) Be careful to distinguish v and V in this figure! 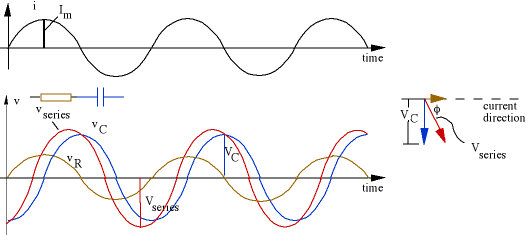
The phasor diagram at right shows us a simple way to calculate the series voltage. The components are in series, so the current is the same in both. The voltage phasors (brown for resistor, blue for capacitor in the convention we've been using) add according to vector or phasor addition, to give the series voltage (the red arrow). By now you don't need to look at v(t), you can go straight from the circuit diagram to the phasor diagram, like this: 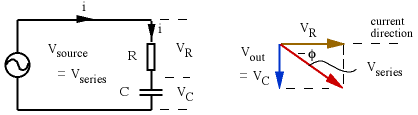
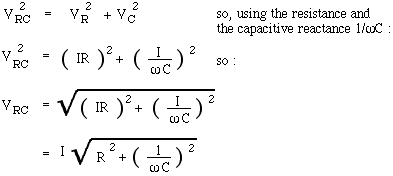
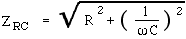 .gif)
Remember how, for two resistors in series, you could just add the resistances: Rseries = R1 + R2 to get the resistance of the series combination. That simple result comes about because the two voltages are both in phase with the current, so their phasors are parallel. Because the phasors for reactances are 90° out of phase with the current, the series impedance of a resistor R and a reactance X are given by Pythagoras' law:
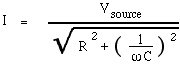 .gif)
So far we have concentrated on the magnitude of the voltage and current. We now derive expressions for their relative phase, so let's look at the phasor diagram again.
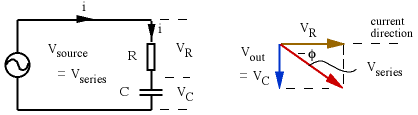
= tan-1 (1/ωRC) = tan-1 (1/2πfRC).
.gif)
.gif)
RL Series combinationsIn an RL series circuit, the voltage across the inductor is aheadof the current by 90°, and the inductive reactance, as we saw before, is XL = ωL. The resulting v(t) plots and phasor diagram look like this.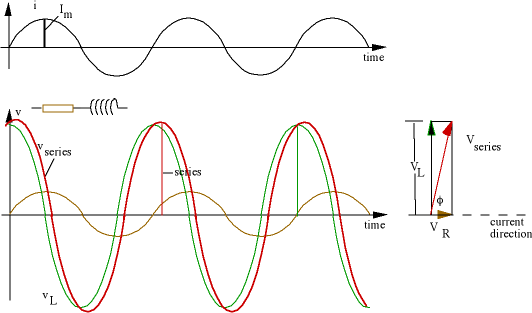
* Exceptions occur at high frequencies (~GHz) where only small value Ls are required to get substantial ωL. In such circuits, you make an inductor by twisting copper wire around a pencil and adjusts its value by squeezing it with your fingers.
RLC Series combinationsNow let's put a resistor, capacitor and inductor in series. At any given time, the voltage across the three components in series, vseries(t), is the sum of these:
Once again, the time-dependent voltages v(t) add up at any time, but the RMS voltages V do not simply add up. Once again they can be added by phasors representing the three sinusoidal voltages. Again, let's 'freeze' it in time for the purposes of the addition, which we do in the graphic below. Once more, be careful to distinguish v and V.
.gif)
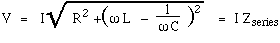
where Zseries is the series impedance: the ratio of the voltage to current in an RLC series ciruit. Note that, once again, reactances and resistances add according to Pythagoras' law:
= R2 + (XL - XC)2. Now let's look at the relative phase. The angle by which the voltage leads the current is
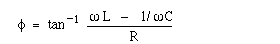
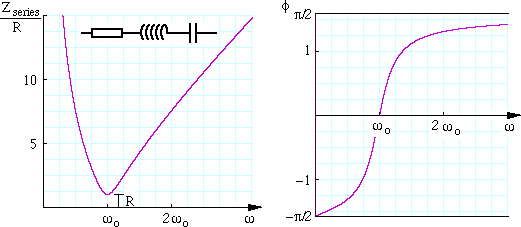
The dependence of Zseries and φ on the angular frequency ω is shown in the next figure. The angular frequency ω is given in terms of a particular value ωo, the resonant frequency (ωo2 = 1/LC), which we meet below.
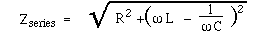 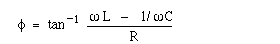
The next graph shows us the special case where the frequency is such that VL = VC. 2.gif)
ResonanceThe graph and the expression for the series impedance show that series impedance goes to infinity at high frequency because of the presence of the inductor, which produces a large emf if the current varies rapidly. Similarly it is large at very low frequencies because of the capacitor, which has a long time in each half cycle in which to charge up. As we saw in the plot of Zseriesω above, there is a minimum value of the series impedance, when the voltages across capacitor and inductor are equal and opposite, ie vL(t) = - vC(t) so VL(t) = VC, so
Complex impedanceYou have perhaps been looking at these phasor diagrams, noticing that they are all two-dimensional, and thinking that we could simply use the complex plane. Good idea! But not original: indeed, that is the most common way to analyse such circuits.The only difference from the presentation here is to consider cosusoids, rather than sinusoids. In the animations above, we used sin waves so that the vertical projection of the phasors would correspond to the height on the v(t) graphs. In complex algebra, we use cos waves and take their projections on the (horizontal) real axis. The phasor diagrams have now become diagrams of complex numbers, but otherwise look exactly the same. They still rotate at ωt, but in the complex plane. The resistor has a real impedance R, the inductor's reactance is a positive imaginary impedance
There are pages on related material at
More to comeWe're still working on this page and shall add more to it as time permits.
|
|
||||||||