Ohm's law and drift velocity in conductors
From Physclips: Mechanics with animations and film.

Drift velocity of charge carriers is related to the DC electric current. This page relates shows how current also depends on the number density of charge carriers, their charge, the cross sectional area of the conductor, the electric field and properties of the material. We begin by introducing a limited analogy using mass and gravitational field as limited analogues of charge and electric field. Alternatively, go straight to the electrical case.

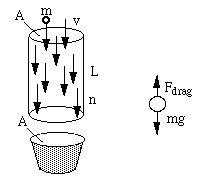
How much rain falls in a bucket per second?

The top of a bucket has area A. Raindrops of mass m are falling at a constant speed v (their terminal velocity). There are n drops per m3. Let's look at the cylinder (length L, area A) above the bucket in the diagram at right. It contains a number of raindrops given by
    n*volume = nAL.
A drop at the very top of the cylinder will leave the cylinder after a time t = L/v. So the time t for all of the raindrops in the cylinder to leave is
    t = L/v
So the rate of rainfall (in kilograms of water per second) into the bucket is
    I = mass/time = (nALm)/(L/v) = nAvm.      (1)
Now let's look at the terminal velocity of the rain drops, which we have assumed constant. The weight pulls them down, and air resistance or drag acts in the upwards direction. If they start from rest, there would be no drag, and their weight would accelerate them downwards until they reached their terminal velocity v. This is the velocity at which there is no further acceleration, because the total force is zero, ie
    weight = drag force.

sketch of rain in bucket

For sufficiently small droplets, the drag force would be proportional to their speed (and we'll conveniently limit discussion to this case). The drag force also depends upon their radius, and on the viscosity of the air, but for raindrops of fixed size, let's include these effects in a constant of proportionality Kdrag. We write:
    Kdragv = Fdrag = weight = mg.
We use this to substitute for v in equation (1) and get:
    I = mass/time = nAvm = nAm2g/Kdrag
Here we note that the current is:
  • proportional to the number of mass carriers/cubic metre of air (n)
  • proportional to the cross sectional area of 'conductor' (A)
  • proportional to the square of the mass on an individual mass carrier (m)
  • proportional to the magnitude of the field that moves them (g)
  • inversely proportional to the proportionality constant for drag (Kdrag)
(The proportionality to mass squared should be qualified: Kdrag is only constant if the size is unchanged, so this proportionality refers to changing the mass by changing the density of the material from which the drops are made.) Let's now derive Ohm's law for gravity and raindrops. We'll need the gravitational potential Vgrav, which is the gravitational potential energy per unit mass, exactly analogous to the electrical case. Take zero potential energy at height h = 0 and we get:
    Vgrav = Ugrav/m = mgh/m = gh.
In the diagram, the cylinder is our resistor (its air is resisting the motion of raindrops). From one end to the other, the height changes by L, so the (gravitational) potential difference across it is Vgrav = gL. So, to get the gravitational version of Ohm's law:
    Vgrav/I = (gL)Kdrag/nAm2g = = LKdrag/nAm2.
Let's separate out the geometrical parameters L and A, and combine the other constants (Kdrag, n and m) into one new constant for this particular air+rain mix:
    Vgrav/I = (Kdrag/nm2).(L/A) = ρ.(L/A),       where ρ = Kdrag/nm2
is the resisitivity of this particular air+rain mix. (In terms of the analogy, this mix is analogous to a particular substance that conducts electricity.) Now let's think about this particular cylinder, with its given length and cross section (analogous to a particular piece of wire).
    Vgrav/I = R       where R = ρL/A,
and where R is the resistance of this particular cylinder of this particular 'substance'. Well, we warned you that the analogy was limited, but it's better than water flowing down rapids!

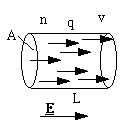
How much charge passes through a conductor per second?

The sketch shows a conductor, length L, cross sectional area A. There are n charge carriers per cubic metre, each carrier having a charge q, and moving at an average speed v. The situation is analogous to the gravitational case except that we have charge q instead of mass m, and an electric field of magnitude E rather than a gravitational field of magnitude g. Inside the cylinder there are nAL charge carriers. The last charge carrier leaves the cylinder after a time t = L/v, so the total charge that leaves the cylinder per unit time is:
    I = (number of charge carriers)*(charge on each)/(time taken for them to leave) = (nAL)q/(L/v) = nAqv.
Let's assume that the average speed v of the carriers is proportional to the electric field E that is moving them, ie write v = const.E. The electric field E is V/L where V is the difference in electrial potential across L, so
    v = const.E, = const.V/L,    so

    I = nAqv = n.A.const.E = const.V.nqA/L.   (3)

Here we note that the current is:
  • proportional to the number of charge carriers/cubic metre (n)
  • proportional to the cross sectional area of the conductor (A)
  • proportional to the magnitude of the field that moves them (E)
  • proportional to the number of charge carriers/cubic metre of conductor (n)

sketch of charge carriers in field

(One must be careful about discussing the dependence on q. Experimentally, one usually cannot vary q. In cases where one can (eg if the charge carriers are ions in a solution), then changing q changes the constant of proportional ity as well.) We can now rearrange equation (3) to give
    V/I = (L/A)(1/(nq.const.)),    which we can write as

    V/I = (L/A)ρ = R

where R is the resistance of this piece of conducting material (whose units are ohms, Ω), and where ρ is the resistivity of the material (whose units are ohm metress, Ωm).

Alternatively, we can take the reciprocal of the terms in the above equation and write:

    I/V = σ(A/L) = G
where G is the conductance of this piece of conductor, (G = 1/R), and where σ is the conductivity of the material,
    σ = n.q.const = 1/ρ.
What if the current doesn't flow uniformly in a conductor? Then we should be interested in the current density or current per unit area: J = I/A. Combining the equations above gives the simplest form:
    J = σE = E/ρ.
This is also the form that is closest to the way in which Ohm expressed his eponymous law originally. The current is parallel to E so in this case the equation has been written in vector form.

Joe Wolfe / J.Wolfe@unsw.edu.au, phone 61- 2-9385 4954 (UT + 10, +11 Oct-Mar).
School of Physics, University of New South Wales, Sydney, Australia.

AC circuits using animations.
Joe's scientific home page
A list of educational links
Music Acoustics site

This page was written partly because the NSW high school syllabus makes some confusing statements about drift velocity. This is discussed under drifton the FAQ for high school physics.

Pic of the author

Creative Commons License This work is licensed under a Creative Commons License.