The wave equation and the speed of sound
Equation (2) gave us 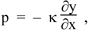 so combining this with the equation above we have so combining this with the equation above we have
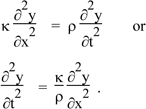 (3) (3)
If you remember the wave in a string, you’ll notice that this is the one dimensional wave equation. When we derived it for a string with tension T and linear density μ, we had
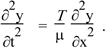
We showed then that this has wave solution with speed 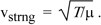
Let’s do it again here: if we seek a solution
y = ym sin (kx − ωt)
and take derivatives, we have

So this is a solution provided that (ω/k)2 = 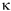 /ρ. Now ω/k is the wave speed (see travelling_sine_wave for revision) so we have, for the speed of sound: /ρ. Now ω/k is the wave speed (see travelling_sine_wave for revision) so we have, for the speed of sound:
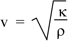
Let's see the analogies: The tension in the string provides a restoring force; so does the elasticity of the medium here. The inertia was provided by the mass per unit length μ of the string, here by the mass per unit volume ρ of the medium.
Although we imagined that our element was air, we have so far only assumed that it is elastic. So this equation is true for longitudinal waves in any elastic medium. For air, we can give a value for the elastic modulus 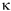 . .
In a page about an ideal gas we show that, during adiabatic expansion and compression, the pressure P and volume V are related
PVγ = constant,
where γ is the adiabatic constant, or the ratio of the specific heat at constant pressure to the specific heat at constant volume, which is about 1.4 for air. (We notice in passing that this is a nonlinear equation.) Taking natural logs of both side, we have
ln P + γ ln V = constant.
Now d(ln x) = dx/x (revise here) so taking derivatives gives us
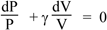
so 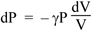
(Although we remarked above that the P(V) equation is nonlinear, we now see that changes in pressure and volume ΔP and ΔV are proportional if ΔP/P is small. A pascal is already a very loud sound at normal frequencies, and atmospheric pressure is about 100,000 Pa, so sound waves in air are usually linear to an excellent approximation.)
The definition of the bulk modulus (see above), expressed as a differential, is
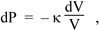
so combining the two equations above we have
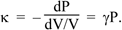
So the speed of sound in an ideal gas is
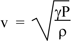
For air at atmospheric pressure (P = 101 kPa) and at T = 20 °C, the density is 1.20 kg.m−3. Taking γ = 1.4 gives a speed of sound of 343 m.s−1.
Specific acoustic impedance
Let’s relate the velocity and pressure, using the solution above:
y = ym sin(kx − ωt)
The particle velocity is
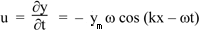
Using equation (2), we have
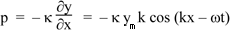
The specific acoustic impedance z of a medium is defined by p/u, so, using the equations above
z = κk/ω.
Above, w e had κ/ρ = v2, above so κ = ρv2. We also had ω/k = v. Substituting these gives the specific acoustic impedance
z = ρv.
Our next step is to relate pressure, flow and power. We do that via the acoustic impedance, which we have just defined as the ratio of the acoustic pressure p to the flow U, where U = uA, where A is the cross-section through which the wave passes. We'll continue on a new support page, on acoustic impedance, power and intensity. See also Compliance, Inertance and Impedance and Acoustic impedance spectrum measurement. |

