|
The specific acoustic impedance z is the ratio of sound pressure to particle velocity, and z = ρv , where ρ is the density and v the speed of sound. (See Acoustic impedance, intensity and power to revise). So for our duct with cross sectional area A, provided that the wave is strictly one dimensional and travelling in one direction, the acoustic volume flow is just U = Au .
For this very special case, we define the characteristic acoustic impedance Z0, where
Z0 = p/U = p/Au = z/A so
Z0 = ρv/A
Of course, there usually are reflections from the other end of the pipe, whether open or closed. So there is a sum of waves travelling to the right and left and quite often these give strong resonances, which is after all how musical wind instruments work. For ducts however, the characteristic acoustic impedance Z0, is the dimensional quantity that scales the acoustic impedance. To see what the impedance spectra of simple ducts and musical instruments look like, see What is acoustic impedance?
It is possible to have no reflections, however. If the pipe length L is very long, then it takes a long time for the reflection to return. So, for the time 2L/v, the duct is effectively infinite. Further, when the echos do eventualy return, they are much attenuated by losses at the wall. (I mention this because, in our research laboratory, we use acoustically infinite acoustical waveguides as calibrations for acoustic measurements. See this web site for the research lab, this page for measurement techniques or this scientific paper for some technical information, if you’re interested.)
Acoustic inertance
Acoustic inertance and acoustic compliance introduce two very important special cases. Both use the idea of a compact region: a region whose dimensions are much smaller than the wavelengths we are considering. As a consequence, the variation in the phase of the sound wave is small in the region, and so the pressure is (approximately) uniform.
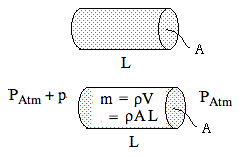What is the impedance of a short cylinder of area A, and length L << λ? The cylinder is vibrating due to an acoustic pressure difference p applied across it. Let it vibrate in the x direction with position y = ym cos ωt, so its acceleration is
a = ∂2y/∂t2 = – ω2ym cos ωt,
From the definition of density ρ = mass/volume, the mass of the cylinder is ρ.V = ρ.AL. The nett force acting on it is p.A. So substitution in Newton's second law (F = ma) gives
pA = ρ.AL.( – ω2ymcos ωt,)
= – ω2ρ.ALym cos ωt = – (pm cos ωt)A
So we have shown that the magnitude of the acoustic pressure required to produce the acceleration described above is pm = ω2ρ.L.ym. (Note that there is no A here: both the force and the mass scale as A.)
This cylinder moves with the particles inside it so, to get the volume flow, we multiply the particle velocity by the area A through which it flows:
U = Au = A∂y/∂t = – Aymω sin ωt,
which tells us that p and U are 90° out of phase. The function cos ωt is 90° ahead of sin ωt. (The cos function has a maximum at t = 0, while the sine function has its maximum a quarter of a period later.) So, when we define the ratio of p to U, we must include this phase difference. The magnitude of the ratio is just
p/U = ω2ρ.L.ym/ωymA = ω.ρ.L/A
So the impedance of a compact region of area A, length L and density ρ is
Z = ω.ρ.L/A and it has a positive phase of 90° (pressure leads flow by 90°).
A comparison of phasors and complex impedance is given in AC circuits. In complex notation, we would write the previous result as
Z = jω.ρ.L/A , where j2 = –1.
Let's check the units: Z is pressure over flow, so (kg.m.s−2/m2)/(m3/s) = kg.m−4s−1. On the right hand side, ωρL/A has units (s−1).(kg.m−3).m/m−2 = kg.m−4s−1. The inertance is just L = ρL/A.
Here, the pressure is required because the mass of the air being accelerated has mass. That's why Z is proportional to ω: vibration at higher frequency requires greater acceleration and therefore greater acoustic pressure. For that reason, an impedance in which the pressure leads the flow by 90° is called an inertive impedance. You can remember the phase difference with this simplified argument: you need to apply the pressure for a while so that the acceleration produces a flow, so the pressure is ahead of the flow.
(You may wonder why the inertance has area in the denominator, when it would be in the numerator for inertia. I did, when I first encountered it. Yes, the mass has A in the numerator. But there are two factors giving A in the denominator: first, our numerator for impedance is pressure, which has A in the denominator, and second, our denominator is U = uA, so another factor A in the denominator.)
Acoustic Compliance
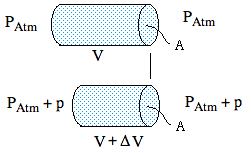 Now let's consider a small volume V, again with dimensions << λ. This time, the applied pressure will compress it, so let's imagine a cylinder of air in a duct with cross section A, that is closed at the right hand end. We apply an acoustic pressure p at the left hand end. This compresses it with an oscillating displacement, a the left end only, y = ym cos ωt. At the instant of my sketch, p is positive and ΔV negative. The volume is changed over time by
ΔV = ymcos ωt = (ΔV)m cos ωt.
The flow U into the volume is – ∂V/∂t, so
U = – ∂/∂t (ΔV)m cos ωt = ω (ΔV)m sin ωt
How much pressure is required to compress a volume of air by ΔV/V? The answer is complicated because, when you compress a gas, its temperature rises, particularly if you compress it so fast that there is insufficient time for heat to be conducted away. In the section on the wave equation for sound, we show that the pressure change p required to produce fractional volume change ΔV/V in a gas initially at pressure P is
where γ, the adiabatic factor (which we derive in Adiabatic compression and expansion) is about 1.4 for air.
Here, the fractional change in volume is (ΔV)m cos ωt /V. Now the pressure at equilibrium is atmospheric pressure PA. So the fractional change in pressure is
pm/PA = – γ (ΔV)m cos ωt/V so pm = – γ PA (ΔV)m cos ωt/V
Here we observe that the pressure (a minus cos function) is 90° behind the flow (a sine function).
So, again, when defining the ratio of Δ p to U, we must include this phase difference. The
magnitude of the ratio is just Δp/U = magnitude of (– γPA (ΔV)m cos ωt /V)/(ω(Δ V)m sin ωt) = γPA/ωV.
So if we set the acoustic compliance C = V/γPA we may write that the impedance Z of an enclosed compact region with entry area A, volume V and a medium at atmospheric pressure and with adiabatic factor γ is
Z = γPA/ωV = 1/ωC and has a negative phase of 90° (pressure lags flow by 90°). In complex notation, we would write this as
Z = – jγPA /ωV = γPA/jωV = 1/jωC
Here, it is gas flowing in that increases the pressure. That's why Z is inversely proportional to omega: vibration at higher frequency has a shorter period, so the amount of gas that flows in during the half period for which flow is inwards is smaller, and produces a smaller pressure.
The air in the confined volume acts like a spring. In analogy with mechanical compliance, a compact enclosed volume is called a compliance and an acoustical impedance in which the pressure lags the flow by 90° is called a compliant impedance. You can remember the phase difference with this simplified argument: you need the flow for a while before the pressure increases much, so the pressure must lag the flow.
You've possibly already thought that a compliance and an inertance could produce resonant oscillations, just like a capacitor and inductance in AC circuits. Correct. A simple example of such an acoustic resonance is a Helmholtz resonance.
The AC electricity analogies
The varying voltage makes the current flow, the varying pressure produces the acoustic flow. Electrical resistance takes power out of the circuit and produces a voltage drop in phase with the (electrical) current. In acoustics, viscous and thermal energy losses at the walls of ducts produce acoustical resistance, with pressure and flow in phase. A capacitor stores electrical charge (integrates current) and produces a voltage which lags current, just like an acoustical compliance (which is sometimes known as acoustic capacitance). An inductor tends to maintain current (it is the electrical analogue of inertia) so an inductance is like an inertance (which is therefore sometimes known as acoustic inductance). The equations are analogous, in both phasor and complex notation. (See AC circuits.)
One important warning about this analogy. Kirchoff's law for electricity should be applied with caution: an acoustical duct is not analogous to a simple short piece of wire. In many electricl circuits, the currents in a wire are often equal at both ends. Consider a duct that is one quarter wavelength long – it could have a flow node at one end and an antinode at the other.
So the fact that air is compressible and has non-negligible mass means that one almost always has acoustic compliance and inertance.
A duct is analogous to an electrical delay or a coaxial cable: both of these have inertive and compliant (inductive and capacitative) terms distributed continuously along their length.
Radiation impedance
What happens when a sound wave gets to the open end of a pipe? In a crude approximation, we could say that, outside the pipe, the pressure is atmospheric, so that it doesn't vary in time, so the acoustic pressure at the open is zero and the wave is reflected with 180° phase change. But of course some sound is radiated from the open end of the pipe so, even if the acoustic pressure is small compared to that inside the pipe, it isn't zero.
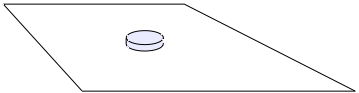 A related problem was first solved by William Strutt (aka Rayleigh). He considered a circular piston (radius a so area A = πa2) oscillating sinusoidally with amplitude xm and frequency ω in a large plane baffle, so its position with respect to the plane of the baffle is x = xmsin ωt. The acoustic flow at the surface of the piston is
The pressure p at the surface of the piston is the pressure due to the impedance Zrad of the radiation field. We should expect that the main contribution to this pressure is the inertance of the air very close to the piston: whereas more distant air is both very slightly moved and slightly compressed/rarefied, the air closest to the piston and just in front of it must move with it. Consider then a volume of air with density ρ, area A and length δ, and let its inertia determine (approximately) Zrad. The force required to move it is
F = mass*acceleration = (ρAδ)(dv/dt) = (ρAδ)(− ω2xmsin ωt)
But from the definition of pressure, F = pA, so the radiation impedance has a magnitude
and its phase is +90°: the radiation pressure is 90° ahead of the flow. For this piston in the infinite flange, δ turns out to be 0.85a.
Now we can consider this piston as approximating the flow at an open pipe. So, for a pipe ending in a large flange, there is an inertance due to the volume of air, with length δ ~ 0.85a, that moves with the wave at the end of the pipe. For a simple, narrow, open pipe, δ is 0.6 a. These are called end effects. For frequencies low enough tht δ << λ, these pipes behave approximately like ideally open pipes, but the radiation inertance at the open end gives them an extra length δ.
Reflection
So, what happens to a wave when it gets to the end of a pipe? Suppose that our pipe is very long, but ends at x = 0, as sketched below. The pipe (x < 0) has a characteristic impedance Z0, and the radiation impedance at the end is Zrad. So the impedance at x = 0 depends on which way one 'looks'. 'Looking out' (at x = 0, but looking at x > 0), the impedance at the end of the pipe is Zrad. 'Looking in' (at x = 0, but looking at x < 0), the impedance at the end of the pipe is Z0. (As we've seen above, Z0 is real: the impedance of a very long pipe is resistive, while Zrad is largely intertive: its impedance is nearly completely imaginary.)
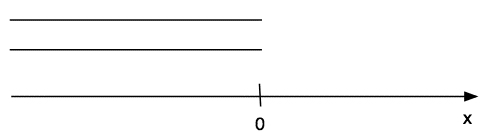Let's suppose that we send a sine wave along the pipe towards the right. Let the pressure due to this wave be p = p>sin (kx − ωt) , where the subscript in the amplitude is to remind us that the wave is travelling to the right (See The wave equation for sound). The flow due to this wave is U = U>sin (kx − ωt) and, as we saw above,
Outside the pipe (at x = 0 but looking out, which we'll write as x = 0+), there is sound radiation away from the pipe. Let's write that the pressure* looking into the radiation field (at x = 0+) is p(0+) = pradsin (− ωt).g(x) , and the flow due out of the pipe due to this wave is U(0+) = Uradsin (− ωt).h(x) . As we also wrote above
remembering that Zrad is almost entirely imaginary, so that prad is almost 90° ahead of Urad in phase—so at least one of them has to be a complex number.
* We can't write a simple one dimensional wave equation here, because the radiation diverges. The geometry very near the pipe end is actually somewhat complicated, but it's not important to this argument. Away from the end, i.e. for kr >> 1, where r is the distance for the end of the pipe, the amplitudes of both prad and Urad go like 1/r and they are in phase: the local geometry approaches that of a plane wave.
Continuity of pressure. Now exactly at x = 0, at the end of the pipe, the pressure just inside the pipe must equal that just outside. (If we didn't satisfy continuity of pressure, we'd have an infinite pressure gradient and so infinite force.) We also have
Continuity of flow: the flow coming out of the pipe (at x = 0−) must equal the flow radiating outwards (at x = 0+). (Continuity of pressure is required because we are not creating or destroying air.) Of course, we can't satisfy those conditions with these two waves: the magnitude of Z0 is much greater than that of Zrad so, if we set the flows equal, the pressures can't be equal.
What happens is no surprise: there is a reflection at the open end: let's write the reflected wave, which travels to the left, as p = p<sin (kx + ωt) and the flow due to this wave is U = U<sin (kx + ωt). So, at x = 0, we have to satisfy the continuity of pressure and flow conditions:
p> + p< = prad and U> − U< = Urad .
(Why the minus sign? Because U> and Urad are flowing out of the pipe while U< is flowing in.) We can use the equations above for Z0 and Zrad to rewrite the equation above right as p>/Z0 − p</Z0 = prad/Zrad. This and the equation above left are two equations that can be solved to give the reflection coefficent at the end:
where we remember that the reflection coefficient is in general a complex number (Zrad is almost completely imaginary). Now, except at very high frequencies,
|Zrad| << Z0, so the reflection coefficient is almost −1: we have reflection with a change in phase of π in pressure, but no change in phase in the flow. This gives us a pressure node (two waves out of phase add approximately to zero) and flow antinode at an open end (two waves in phase add to give a maximum).
So, we have a reflection at the open end of a pipe: very useful the standing waves in musical instruments, the voice and elsewhere. Examples, explanations and animations are given in Open and Closed Pipes and Pipes and Harmonics.
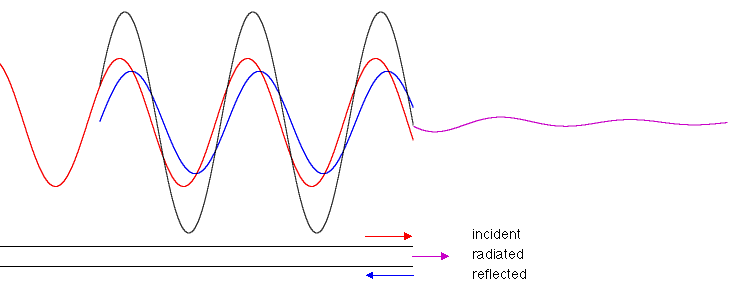
In the sketch, a wavetrain p> in red is shown reflecting at the end of a pipe: p< is in blue and their sum, the standing wave, in black. The radiated wave is purple.
Reflection at a closed end is somewhat easier. If the pipe is ideally closed, then the conservation of flow must mean that U> and U< add to zero, which means that they are out of phase by π. Their pressures are in phase, so the closed end of a pipe has an antinode in pressure and a node in flow.
Compliance and inertance of resonances in pipes
Let's apply an oscillating pressure to one end of an open pipe. At very low frequency (wavelengths much longer than the pipe), all of the air in the pipe moves forwards and backwards together, accelerated by the pressure (pressure leads flow). It's acting like an unconstrained compact mass, just as we saw for the short open pipe above. So at low frequency, its impedance is inertive. It goes to zero at zero frequency, but the impedance rises (at first) with increasing frequency, because the acceleration is increasing with frequency. The first resonance we reach has a very high impedance – a quarter-wave resonance.
Now let's increase the frequency above that first resonance. Now, much of the air doesn't have time to get out in half a cycle and air near our driving point is compressed and rarefacted by the pressure. So its impedance is compliant. Inertive below the first resonance (and others); compressive above. At low frequency, it's like driving a mass-spring system from the spring side.
Now let's input oscillating flow into a closed pipe. At very low frequency, flow into the pipe gradually increases the pressure (flow leads pressure). It's acting like a sealed compact volume: it's compliant. At zero frequency, its impedance goes to infinity because its capacity to absorb flow is finite. The impedance falls (at first) with increasing frequency. It gets very low at the first resonance - again a quarter-wave resonance. Above that resonance, we notice the inertia of the air: the impedance becomes inertive. Compliant below the first resonance (and others) and inertive above. At low frequency, it's like driving a mass-spring system from the mass side.
See Acoustic impedance of pipes. See Open vs closed pipes.
Impedance Maching
From the diagram above, we can see that, when the incident wave reaches the transition from high impedance in the duct to low impedance in the radiation field, most of the power in the incident wave is reflected, rather than transmitted. Higher transmission can be achieved by inserting between the two a region of intermediate impedance. (To continue the electric analogy from above, this may be compared with impedance matching stages or transformers.)
The bell on a trombone functions as an impedance transformer. This can readily be demonstrated by disconnecting the bell, which makes the instrument much softer. It also changes the timbre substantially, because the bell transmits waves whose wavelength is small compare with the radius of curvature of the bell profile.
Another good example is a closed-open pipe. For a wavelength four times the length of the pipe (and for odd multiples of this frequency), the impedance is very high at the closed end and very low at the open end. (More about these resonances.) For this reason, the vocal tract is a good impedance matcher for some frequencies: the resonances in the tract produce formants in the output sound. The ear canal or auditory meatus also has resonances that act as impedance transformers for two bands of frequencies. See also this section of our FAQ.
More information
|
