On the page on the sound wave equation, we wrote a solution for the particle displacement y as a function of position x and time t:
y = A sin (kx − ωt)
where A is the displacement amplitude, k is the wave number (k = 2π/λ) and ω is the angular frequency (ω = 2πf). We also showed that the particle velocity u and the acoustic pressure p are given by
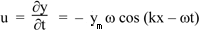 and
and 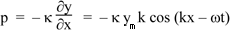
where κ is the adiabatic bulk modulus. We defined z as p/u, so
z = κk/ω.
We also showed on that page that κ/ρ = v2, above so 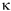 = ρv2 where ρ is the density. We also had ω/k = v. Substituting these gives
= ρv2 where ρ is the density. We also had ω/k = v. Substituting these gives
z = ρv.
Values for air and water. For air, the density is 1.2 kg.m−3 and v is 343 m.s−1, so the specific acoustic impedance for air is 420 kg.s−1.m−2 = 420 Pa.s.m−1. The values for condensed phases are usually much higher than those of gases. For (fresh) water, the density is 1000 kg.m−3 and v is 1480 m.s−1, so the specific acoustic impedance for water is 1.48 MPa.s.m−1. For human soft tissues, the values are comparable with that of water.
Volume flow and acoustic impedance
Let’s now consider a one dimensional wave passing through an aperture with area A. The volume flow U is the volume passing per second through the aperture. If the flow moves a distance dy = udt, then the volume passing through is Ady, so
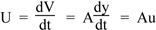
The acoustic impedance Z is the ratio of sound pressure to volume flow, so provided that the wave is only one dimensional, we should have
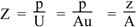
In practice, it’s usually more complicated: if you send a wave into a pipe with uniform cross section A, there are usually reflections from the other end of the pipe, whether open or closed. So there is a sum of waves travelling to the right and left*. In the absence of reflections, we call this the characteristic acoustic impedance Z0. So
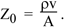
It is possible to have no reflections, however. If the pipe is very long, then it takes a long time for the reflection to return and, when it does, it is much attenuated by losses at the wall. I mention this because, in our research laboratory, we introduced acoustically infinite acoustic waveguides as calibrations for acoustic measurements. The technique allows precise measurements of impedance spectra over 9 octaves using a single impedance head. It is described in this scientific paper.
* The reflections and resultant standing waves are very important in musical instruments. On the page What is acoustic impedance?, we give examples of acoustic impedance spectra for pipes and for musical instruments, and explain the importance of the quantity in music acoustics.