Transformers From Physclips:
Mechanics with animations and film.
|
In the photograph, note that the coil on the left has fewer coils
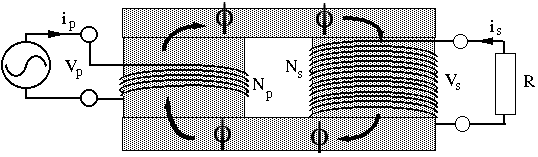
than that at right (the insets show close-ups). The sketch and circuit
show a step-up transformer. To make a step-down transformer, one
only has to put the source on the right and the load on the left.
(Important safety note: for a real transformer, you could
only 'plug it in backwards' only after verifying that the voltage
rating were appropriate.) So, how does s transformer work?
The core (shaded) has high magnetic permeability (ie a material
that forms a magnetic field much more easily than free space does,
due to the orientation of atomic dipoles). The result is that the
field is concentrated inside the core, and almost no field lines
leave the core. If follows that the magnetic flux φ through
the primary and secondary are equal, as shown. From Faraday's law,
the emf in each turn, whether in the primary or secondary coil, is −dφ/dt. If we neglect resistance
and other losses in the transformer, the terminal voltage equals
the emf. For the Np turns of the primary, this gives
For the Ns turns of the secondary, this gives
Dividing these equations gives the transformer equation
where r is the turns ratio. What about the current? If we neglect losses
in the transformer (see the section below on efficiency), and if we
assume that the voltage and current have similar phase relationships
in the primary and secondary, then from conservation of energy we may
write, in steady state:
Power in = power out, so
VpIp = VsIs, whence
Is/Ip = Np/Ns = 1/r.
So you don't get something for nothing: if you increase the voltage,
you decrease the current by at least the same factor. Note that, in
the photograph, the coil with more turns has thinner wire, because
it is designed to carry less current than that with fewer turns.
In some cases, decreasing the current is the aim of the exercise.
In power transmission lines, for example, the power lost in heating
the wires due to their non-zero resistance is proportional to the
square of the current. So it saves a lot of energy to transmit the
electrical power from power station to city at very high voltages
so that the currents are only modest.
|

Photograph of a demountable transformer, used for
demonstrations
Schematic of step-up circuit
|
Finally, and again assuming that the transformer is ideal, let's ask what the
resistor in the secondary circuit 'looks like' to the primary circuit. In the
primary circuit:
Vp = Vs/r and
Ip = Is.r so
Vp/Ip = Vs/r2Is =
R/r2.
R/r2 is called the reflected
resistance. Provided that the frequency is not too high, and provided that
there is a load resistance (conditions usually met in practical transformers),
the inductive reactance of the primary is much smaller than this reflected resistance,
so the primary circuit behaves as though the source were driving a resistor of
value R/r2. This allows transformers to be used as impedance matchers. A load with low input impedance can be matched to circuit with high output impedance using a step down transformer.
We have been asked: how does the transformer equation fit with Ohm's law? If the secondary voltage is twice the primary, why isn't the secondary current twice the primary? First, one can only apply Ohm's law to resistors and, if there were (only) a resistor on both primary and secondary sides, then the voltage on both sides would be zero. Usually, the primary coil is connected to an AC source, which does not obey Ohm's law. For instance, the mains supply is 240 volts if the current is zero, and not far from 240 volts if the current is 1 amp.
Efficiency of transformers
In practice, real transformers are less than
100% efficient.
- First, there are resistive losses in the coils (losing power I2.r).
For a given material, the resistance of the coils can be reduced by making
their cross section large. The resistivity can also be made low by using
high purity copper. (See Drift velocity and Ohm's
law.)
- Second, there are some eddy current losses in the core. These can be reduced
by laminating the core. Laminations reduce the area of circuits in the core,
and so reduce the Faraday emf, and so the current flowing in the core, and
so the energy thus lost.
- Third, there are hysteresis losses in the core. The magentisation and demagnetisation
curves for magnetic materials are often a little different (hysteresis or
history depedence) and this means that the energy required to magnetise the
core (while the current is increasing) is not entirely recovered during demagnetisation.
The difference in energy is lost as heat in the core.
- Finally, the geometric design as well as the material of the core may be
optimised to ensure that the magnetic flux in each coil of the secondary
is nearly the same as that in each coil of the primary.
More about transformers: AC vs DC generators
Transformers only work on AC, which is one of the great advantages of AC. Transformers
allow 240V to be stepped down to convenient levels for digital electronics (only
a few volts) or for other low power applications (typically 12V). Transformers
step the voltage up for transmission, as mentioned above, and down for safe distribution.
Without transformers, the waste of electric power in distribution networks, already
high, would be enormous. It is possible to convert voltages in DC, but more complicated
than with AC. Further, such conversions are often inefficient and/or expensive.
AC has the further advantage that it can be used on AC motors, which are usually
preferable to DC motors for high power applications.
|