|
|
|||
|
|
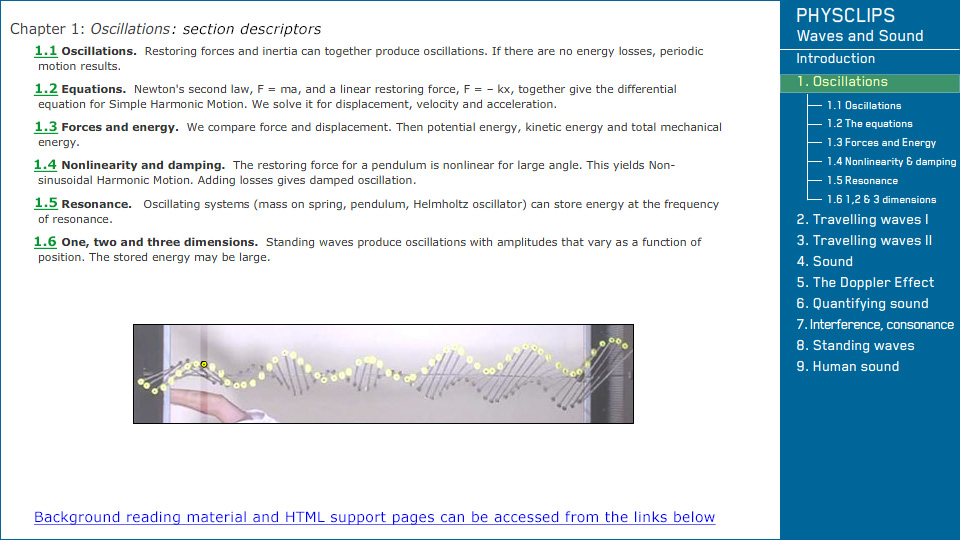
|
| Links to supporting pages and teachers' resources | |
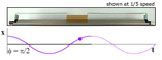
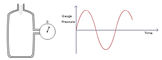
| Background to Oscillations Inertia plus a restoring force produces oscillations. The mechanical equation for Simple Harmonic Motion. Initial conditions. Cyclic and angular frequency. Mechanical and kinetic energies. The simple pendulum. A nonlinear pendulum. Damped oscillations. Forced oscillations. Resonance in one, two and three dimensions. includes |
 |
 |
|
| Strings, standing waves and harmonics | 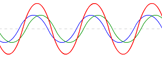 |
| Chladni patterns |  |
| Inertia and the second law |  |
| Kinematics of Simple Harmonic Motion |  |
| Hooke's law and elasticity | |
| Revise calculus | 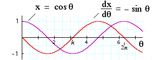 |
| Solving Differential Equations Methods for solving differential equations. First order with constant coefficients. Second order and simple harmonic motion. Damped and forced oscillation. Partial differential equations: the wave equation. |
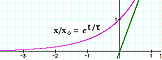 |
| Phasor addition Phasor representation of Simple Harmonic Motion. Adding phasors with different amplitudes and phase but equal frequency. Constructive and destructive interference. What if frequencies are different? Phasor and Lissajous representations compared. |
 |
| Laboratory |
 |
|
||||